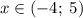Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
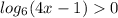решаем данное неравенство.
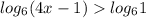
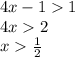
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
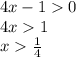
рассматриваем оба неравенства и находим область пересечения интервалов
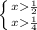x∈ [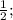 
+∞ [
7. 
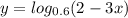значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
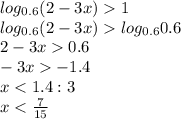
находим область пересечения обоих условий,
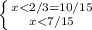x∈ ] -∞; 7/15 [
8. 
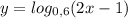область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
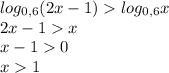
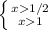x∈ ] 1; +∞ [
1) x^2 >= 196
x <= -14 U x >= 14
2) x(x+5)(2-6x)(2x-4) <= 0
Разделим неравенство на (-4). При этом знак неравенства поменяется.
x(x+5)(3x-1)(x-2) >= 0
По методу интервалов, особые точки: -5, 0, 1/3, 2.
x ∈ (-oo; -5] U [0; 1/3] U [2; +oo)
3) Это НЕ неравенство
4) x^2*(2+3) > 0
5x^2 > 0
Это неравенство истинно при любом x, кроме 0.
x ∈ (-oo; 0) U (0; +oo)
5) (x+2)/(x-4)^2 >= 0
x ≠ 4
(x - 4)^2 > 0 при любом x, не равном 4, поэтому можно на нее умножить.
x + 2 >= 0
x ∈ [-2; 4) U (4; +oo)
Имеем 3 интервала: (-∞; -4), (-4; 5) и (5; +∞). Определим знак выражения на каждом из них:
ответ: