2cos²(π/4-2α)=cos2(π/4-2α)+1=cos(π/2-4α)+1=1+sin4α
Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:
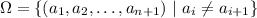
Из условия следует, что каждый исход равновероятен.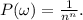 
Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок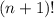 
. Теперь можно считать вероятность:
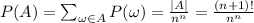
2cos^2(п/4-2а)=sin4a+1
Докажим это тождество:2cos^2(п/4-2а)=1 + cos(2(п/4-2а))
2cos^2(п/4-2а)=1+cos(п:2-4а)=
2cos^2(п/4-2а)=1+sin4a
ответ: Тождество доказано