Абсцисса вершины ищется по формуле -в/2а, и равна по условию 3.значит, -в=6, в= -6; для того, чтобы найти с, подставим в формулу параболы у =ах²+вх+с координаты вершины, получим
1*3²-6*3+с=3, отсюда с =12
Парабола имеет вид у=х²-6х+12и пересекается с прямой у =2х, находим координаты точек пересечения, приравняв у
х²-6х+12=2х; х²-8х+12=0
По теореме, обратной теореме Виета, х₁=2; х₂=6, тогда у₁=2*2=4; у₂=2*6=12
Итак, искомые точки (2;4) и (6;12)
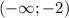
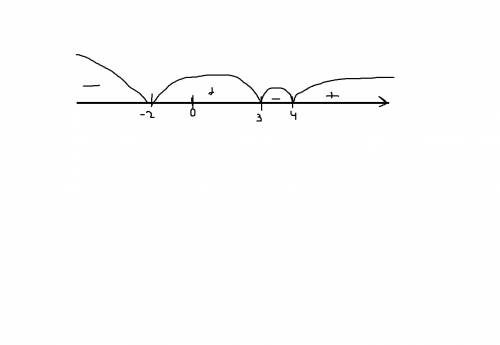
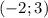(рис. 2)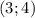
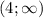
Возможный вывод: d
36 + x2
Используйте частное правило
d
dx dr, где u = x и v = x2 + 36:
(36+x2)( -00) - ((36+ x2)) dx (36 + x2)2
Производная от x равна 1:
-х( (36+х2))+ 1 (36+ x2) x2)
(36 + x2)2
Упростите выражение:
36 + x2 - ( 4 (36+х2))
(36 + x2)2
Дифференцируйте сумму термин за термином:
36 + x2 - (36) + (x2)
(36 + x2)
Производная от 36 равна нулю:
36+x2-x(4 (x2) + 0)
(36 + x2)2
Упростите выражение:
(40+)
(36 + x2)2
Используйте правило мощности, --- (x") = n.x" 1, где = 2.
dx
(x2) = 2x:
36+x?-2xx
(36 + x2)2
Упростите выражение:
36 - x2
(36 + x2)2
ответ:(2;6)
Объяснение: