x∈[-4 ; 4]
Объяснение:
Решим каждое неравенство в отдельности:
1) 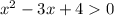
Приравняем к 0, чтобы найти корни уравнения:

Это обычное квадратное уравнение, значит, сначала найдем дискриминант:
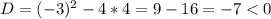
D < 0, а значит, вещественных корней нет.
Значит, неравенство выполняется ВСЕГДА или НИКОГДА. Проверим, подставив любое число в уравнение. Например, x = 10:
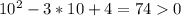
Получили значение больше 0, значит, неравенство выполняется ВСЕГДА при ЛЮБЫХ значениях x
x ∈ (-∞ ; +∞)
2) 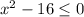
Приравняем к 0 и найдем корни:

Получили 2 корня. Наносим их на координатную ось, ставим 2 точки: -4 и 4. Далее расставляем знаки функции на участках (путем подстановки любого числа из этого участка: до -4 возьмем -10, подставим в уравнение и получим положительное число → +; между -4 и 4 возьмем 0, подставим, получим отрицательное число → –; от 4 и далее возьмем 10 и получим положительное число → +). Нам нужен тот участок, в котором функция принимает ОТРИЦАТЕЛЬНОЕ значение, т.е. там где стоит минус.
Значит ответ: x∈[-4 ; 4]
Скобки квадратные, т.е. неравенство строгое (есть знак равно).
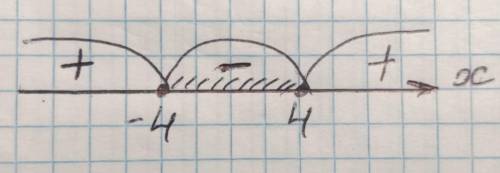
1. По условию - 21<х>42
2. методом исключения: исключает от 21 до 42 все числа, которые не делятся на 3 и у нас остаеются: 24, 27, 30, 33, 36 и 39,
3. Делим каждое из этих чисел на 7 и смотрим, где будет остаток 1, то число и подходит.
24:7=3(ост.3) - не подходит
27:7=3 (ост.6) - не подходит
30:7=4 (ост.2) - не подходит
33:7=4 (ост.5) - не подходит
36:7=5 (ост.1) - ПОДХОДИТ
39:7=5 (ост.4) - не подходит
4. Проверяем: 36<42? - да
36>21? - да
36:3? - да
36:7 с остатком 1? - да
x∈[-4;4]
Объяснение: