Скорость третьего Х отрывается все от временной точки, когда третий догонит второго (время t) (первый ехал на 1 час больше (t+1) третий на один час меньше (t-1), это когда 15*t=X*(t-1) (их пройденные пути выравняются) второе уравнение 21*(t+9+1)=X(t+9-1) итого система 15t=Xt-X -> 15t-Xt=-X -> t(15-X)=-X -> t=-X/(15-X) =X/(X-15) 21t+210=Xt+8X (во второе подставим t) 21X/(X-15)+210=(X^2)/(X-15)+8X избавляемся от знаменателя (Х-15) 21X +210(X-15)=X^2+8X(X-15) 21X+210X-3150=X^2+8X^2-120X все вправо 9x^2-351x+3150=0 (сократим на 9) x^2-39x+350=0
D=1521-1400=121 (корень 11) x1=(39+11)/2=25 x2=(39-11)/2=14 (заведомо неверный, поскольку его скорость явно выше скорости первого (21), раз он его догнал) итого Х=25 км/ч
Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть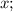
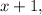
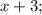
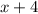- пять последовательных натуральных чисел, тогда их сумма равна:
Очевидно, что каждое слагаемое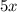
и 
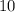делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть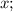
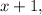
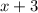- четыре последовательных натуральных числа, тогда их сумма равна:
Очевидно, что первое слагаемое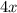
делится на 4, а второе слагаемое 
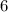не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть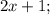
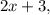
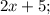
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое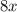
и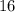 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть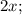
; 
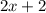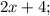
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
Очевидно, что каждое слагаемое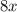
и 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.