Начертим рисунок. Изобразим прямоугольный треугольник, один катет которого расположен горизонтально (на восток), а второй вертикально (на юг).
Для решения задачи применим теорему Пифагора.
Итак, скорость первого велосипедиста обозначим х км/ч,
скорость второго (х+4) км/ч.
Первый за 1 час проехал расстояние хкм/ч * 1 ч =х км
а второй (х+4)км/ч * 1 ч =х+4 км
Расстояние между велосипедистами (это гипотенуза прямоугольного треугольника) через 1 час оказалось 20 км.
Составим уравнение для решения задачи:
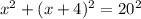
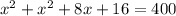
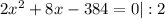
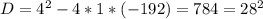
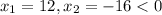
x=12(км/ч)-скорость первого
х+4=12+4=16(км/ч)-скорость второго
Объяснение:
a = 1 (коэффициент при x^2)
b = 6 (коэффициент при x)
c = -5 (свободный элемент)
1) Вершина параболы находится по формуле
xв = -b/2a = -6/(2*1) = -3
yв находится подстановкой хв в исходное уравнение
ув = (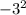
) + 6 *(-3) -5 = 9 -18 - 5 = -14
Координаты точки вершины (-3, -14)
2) Пересечение с ОХ происходит когда y = 0
+ 6x - 5 = 0
D = 36 + 5*4 = 56
Тогда пересечение с осью ОХ происходит в точках:
x1 = 
x2 =
3) Пересечение с ОУ происходит когда x = 0
y = 0 + 0 -5 = -5
(0, -5)
4) x = m
y = 3
3 =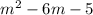 
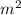- 6m - 8 = 0
D = 36 + 32 = 68
m1 =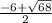 
m2 = 
5)
Відповідь:х⁴+2x²-3=0( нехай х²= t)
D= 2² - 4*4*(-3)= 4+48=52 ; √52=7.2
X(Мал 1) = -2+7.2/2=2.6
X(Мал 2)= -2-7.2=4.6
X²= 2.6. X²=4.6
X=±1.6 x=±2.1
Пояснення: