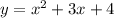
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
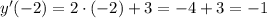
Уравнение касательной имеет вид:
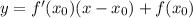
Подставим значение 
Итак, уравнение касательной заданной функции: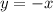 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
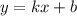численно равен тангенсу угла наклона 
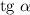с положительным направлением оси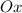 
В найденной касательной коэффициент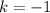 
, следовательно, 
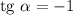при 
или 
ответ: или
4/9
Объяснение:
Чтобы число делилось на 18 необходимо, чтобы оно одновременно делилось на 9 и на 2.
Чтобы число делилось на 9, необходимо чтобы сумма его цифр делилась на 9. Так как 1+2+...+9=45, а 45 делится на 9, то и любое девятизначное число, составленное из этих цифр делится на 9.
Чтобы число делилось на 2, необходимо чтобы его последняя цифра делилась на 2. Всего на последнем месте может стоять любая из 9 цифр, но желательно, чтобы там стояла какая-либо из цифр 2, 4, 6, 8. То есть благоприятных событий - 4, общее число событий - 9.
Итак, число всегда делится на 9 и с вероятностью 4/9 делится на 2. Значит и на 18 оно будет делится с вероятностью 4/9.