Как правильно вставлять значение x в уравнение ${x}^{2}$ если x = -1; если вставлять со скобками (-1)^2 то ответ 1, а если без -1^2 ? ? у меня в вот такое уравнение нужно вставить -1 вместо х $\frac{x ^{3} + 2x ^{2} - 3x }{x}$

👇

Ответ:

Marina20012608

19.01.2022

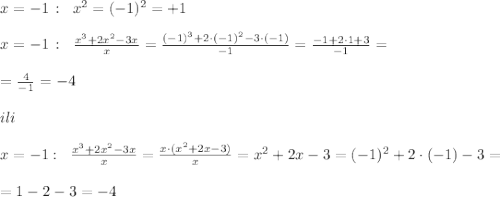
$x=-1\, :\; \; x^2=(-1)^2=+1\\\\x=-1\, :\; \; \frac{x^3+2x^2-3x}{x}=\frac{(-1)^3+2\cdot (-1)^2-3\cdot (-1)}{-1}=\frac{-1+2\cdot 1+3}{-1}=\\\\=\frac{4}{-1}=-4\\\\ili\\\\x=-1:\; \; \frac{x^3+2x^2-3x}{x}=\frac{x\cdot (x^2+2x-3)}{x}=x^2+2x-3=(-1)^2+2\cdot (-1)-3=\\\\=1-2-3=-4$

4,7(58 оценок)

Ответ:

yurinskayat1

19.01.2022

Объяснение:

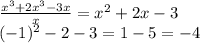
$\frac{x^3+2x^3-3x}{x} =x^2+2x-3\\(-1)^2-2-3=1-5=-4$

4,6(57 оценок)

Открыть все ответы

Ответ:

tinytigerkar

19.01.2022

Объяснение:

При n=1 верность неравенства очевидна.

При n=2, получаем известное верное неравенство, оно нам понадобится.

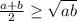
$\frac{a+b}{2} \geq \sqrt{ab}$

Теперь докажем, что из верности неравенство верно для n=m, следует его верность для n=2m.

В самом деле, пусть неравенство верно для n=m. Нам нужно доказать, что тогда верно и неравенство

$\frac{a_1+a_2+...+a_m+a_{m+1}+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}$

Так как неравенство верно для n=m (по индуктивному предположению), можем записать такие два неравенства:

$\frac{a_1+a_2+...+a_m}{m} \geq \sqrt[m]{a_1a_2...a_{m}} \\\frac{a_{m+1}+a_{m+2}+...+a_{2m}}{m} \geq \sqrt[m]{a_{m+1}...a_{2m}} \\$

Теперь сложим эти неравенства и разделим обе части полученного на 2. Получится вот такое неравенство:

$\frac{a_1+a_2+...+a_{2m}}{2m} \geq \frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2}$

Но использовав неравенство для n=2 получаем:

$\frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2} \geq \sqrt{\sqrt[m]{a_1a_2...a_{m}}\sqrt[m]{a_{m+1}...a_{2m}}} =\sqrt[2m]{a_1a_2...a_{2m}}$

Тогда и подавно

$\frac{a_1+a_2+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}$

А теперь, следуя за Коши (который как раз первым доказал это неравенство), заметим, что из доказанного выше следует, что если неравенство верно для 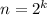n=2^k (где k - натуральное), то оно верно и для 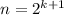$n=2^{k+1}$ . Действительно, чтобы доказать это, достаточно положить 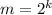m=2^k , тогда 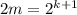$2m=2^{k+1}$ и неравенство также верно. А так как неравенство верно для n=2, то по индукции отсюда получаем верность неравенства для всех остальных степеней двойки, то есть для чисел вида 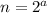n=2^a при любом натуральном . Это утверждение назовём Леммой 1.

Осталось доказать, что из верности неравенства для n=k, следует его верность для n=k-1. Это будет наша Лемма 2.

Ну что же, раз в задании дана такая превосходная подсказка - воспользуемся ей. Найдём такой x, о котором идёт речь в задании. Он выражается из данной в условии формулы очевидным образом, не буду на этом останавливаться:

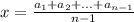
$x=\frac{a_1+a_2+...+a_{n-1}}{n-1}$

Теперь пусть неравенство верно для произвольного n=k.

Применим это неравенство к числам 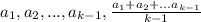$a_1, a_2, ... , a_{k-1}, \frac{a_1+a_2+...a_{k-1}}{k-1}$ :

$\frac{a_1+...+a_{k-1}+\frac{a_1+...+a_{k-1}}{k-1} }{k} \geq \sqrt[k]{a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}}$

Что получится в левой части мы знаем - среднее арифметическое чисел 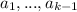$a_1, ... , a_{k-1}$ . Далее возводим неравенство в степень k и преобразовываем:

$\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^k\geq a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}\\\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^{k-1}\geq a_1...a_{k-1}\\\frac{a_1+...+a_{k-1}}{k-1}\geq \sqrt[k-1]{a_1...a_{k-1}}$

Получили как раз неравенство для n=k-1.

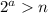Собственно, неравенство можно считать доказанным. Лемма 1 и Лемма 2 решают вопрос для любого n. В самом деле, возьмём произвольное натуральное n. Очевидно, найдётся такое натуральное , что 2^an . Неравенство верно для этой степени двойки (Лемма 1). Но оно верно также и для всех натуральных чисел меньших её, это по индукции следует из Леммы 2. Тогда неравенство верно и для нашего произвольно выбранного n.