Функция f(x)=4x³+8x²+9;
а) найти промежутки возврастания(убывания) ;
б ) найти критические точки .
f '(x) = (4x³+8x²+9) ' =(4x³) ' +(8x²) '+( 9) '=4(x³) ' +8(x²) '+0 =4*3x² +8*2x =
12x(x+4/3) ; D(f '(x) ) : x ∈ R
Функция убывает (↓) ,если f '(x) ≤ 0 ( возрастает, если f '(x) ≥ 0 )
12(x+4/3)x ≤ 0 ⇒ x∈ [ - 4/3 ; 0 ]
[ - 4/3 ] [0]
f ' (x) "+" " -" " +"
f(x) ↑ ↓ ↑
Функция возрастает промежутках ( -∞ ; -4/3] и [ 0 ; ∞) ;
убывает в промежутке [ - 4/3 ; 0]
- - - - - - -
б) Критические точки : f '(x) = 0 ⇔ (x+4/3)x =0 ⇒ x = - 4/3 и x=0 , притом эти критические точки являются точками экстремумов .
x = - 4/3 точка максимума ; x=0 _точка минимума.
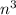 , по условию
, по условию 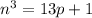 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
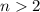 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 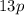 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 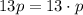 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 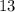 и
и 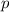 , либо
, либо 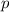 и
и 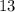 .
.
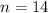 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 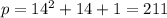 .
.  - действительно простое число, так что
- действительно простое число, так что 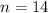 нас устраивает.
нас устраивает.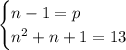
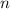 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 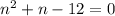 , у которого только один натуральный корень
, у которого только один натуральный корень 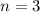 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 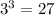
Объяснение:
f(x)=4x^3+8x^2+9
в) f'(x)=(4x^3+8x^2+9)'=12x²+16x
Критические точки функции - это те её точки, при которых производная равна нулю или не существует
f'(x)=0⇒12x²+16x⇒4х(3х-4)=0⇒х1=0;х2=4/3
Так как точек, при которых производная не существует нет,
критические точки: 0; 4/3
+ - +
а)
0 4/3
Функция возрастает на (-∞;0]∪[4/3;+∞)
Функция убывает на [0;4/3]