Задание №1.
1. На березе растут яблоки - Невозможное.
2. При бросании игральной кости выпала цифра 6 - Равновозможное.
3. За летом наступает осень - Достоверное.
Задание №2.
Всего двухзначных чисел у нас - 90 (от 10 до 99). Проще всего рещать в лоб, выбирая подходящие числа:
1) Нулём оканчивается каждое десятое из них, т.е. всего таких чисел 9. P = 9/90=0,1
2) Из одинаковых цифр состоит каждое одиннадцатое из них, начиная с 11, т.е. всего таких чисел 9. P = 9/90=0,1
3) Больше 27 и меньще 46 - всего 18 чисел, т.е. P =18/90=0,2
4) Квадратами целого числа являются 16, 25, 36, 49, 64, 81 - итого 6. P = 6/90=1/15
Задание №3.
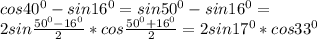
Объяснение:
в низу
Объяснение:
1. Перетворіть вираз з(ь – 6, 5) у такий, що тотожно дорівнює йому. 2. Запишіть вираз т – (6-n+b) без дужок. 3. Спростіть вираз 15-(a-4). 4. Розкрийте дужки й зведіть подібні доданки у виразі 4b – (76 + 2). 5. Виконайте тотожне перетворення виразу 2,5 (2k + 4а – 2). 6. Спростіть вираз 2(a+1) +а та знайдіть його значення, якщо a=1. 7. Доведіть тотожність (2x +1)-(1-2x) = 4х. 8. Зведіть подібні доданки у виразі -4+32+62. 9. Спростіть вираз -(-5)-(-y). 10. Доведіть, що вираз 7(a-b)+7(b – а) тотожно дорівнює 0. 11. Доведіть тотожність -(2-(-x)+2+x = 0. 12. Доведіть, що сума виразів 13c + 3 і 2c +3 ділиться на
ответ:√(x - 2) является x > = 2.
Объяснение:
Опишем функцию для нахождения области определения
Функция является сложной, так как выражение под корнем имеет выражение х - 2;
Функция имеет квадратный корень;
Из квадратного корня, не возможно извлечь отрицательное число;
Область определения функции - это те значения х, которое можно подставить в функцию. Отсюда делаем вывод, что областью определения функции является выражение под корнем больше или равно 0.
Находим область определения функции
Выражение под корнем равно х - 2. Так как, оно должно быть больше или равно 0, то отсюда получаем:
x - 2 > = 0;
Известные значения переносим на одну сторону, а неизвестные на другую сторону. При переносе значений, их знаки меняются на противоположный знак. То есть получаем:
x > = 0 + 2;
x > = 2;
Значит, областью определения функции y = √(x - 2) является промежуток x > = 2;
Проверка
Подставим значение х = 6, которое удовлетворяет условию x > = 2 в функцию y = √(x - 2), тогда получим:
y = √(6 - 2);
y = √4;
y = 2;
Значит, при х > = 2 из квадратного корня извлекаются положительные числа. Если же, если было бы < 2, то квадратный корень из отрицательного числа не извлекается.