Підсумкова контрольна робота 10 клас геометрія Варіант-2 ( Підготовка до річної к/р )

Завдання 1-6 мають по чотири варіанти відповідей, з яких тільки одна правильна. Оберіть правильну, на вашу думку, відповідь та запишіть у зошиті номер завдання та відповідну літеру.
1. (0,5б.) Дано паралельні прямі а і в. Скільки існує площин, які проходять через пряму а і паралельні прямій в?
А) одна Б) безліч В) жодної Г) дві
2. (0,5б.) Знайдіть довжину відрізка АВ, якщо А(3;-2;5) і 2(-1;1;5).
А) 11 Б)√5 В) 5 Г) √17.
3. (0,5б.) Яка з геометричних фігур не може бути паралельною проекцією двох паралельних прямих?
А) дві точки Б) дві паралельні прямі В) пряма Г) відрізок
4. (0,5б.) Яка з точок належить осі ординат?
А) С(0;9;0) Б) К(0;0;-8) В) М(7;0;1) Г) (4;0;0)
5. (0,5б.) З точки А, віддаленої від площини α на 9 см, проведено похилу АВ до цієї площини. Знайдіть довжину похилої АВ, якщо довжина її проекції на площину α дорівнює 12см .
А) 21см Б) 15см В) 13см Г) 3√7 см.
6. (0,5б.) Яка з точок симетрична точці А(3; -4; 2) відносно площини УZ?
А) С(-3;-4;2) Б) К(3;-4;-2) В) М(3;4;2) Г) (-3;-4;-2)

7. (по 0,5б. за правильну відповідність) Установіть відповідність між заданими векторами а ⃗ і в ⃗ (1-4) та правильними твердженнями (А-Д).
1. а ⃗(-4;1;2) і в ⃗(-1;2;2) А Вектори а ⃗ і в ⃗ перпендикулярні
2. а ⃗(3;4;-2) і в ⃗(-4;2;-2) Б Різницею векторів а ⃗ і в ⃗ є вектор с ⃗(-5;-1;0)
3. а ⃗(-8;2;-2) і в ⃗(4;-1;1) В Вектори а ⃗ і в ⃗ протилежно напрямлені
4. а ⃗(2;-3;-1) і в ⃗(-1;3;2) Г |а ⃗ |-|в ⃗ |=0
Д Скалярний добуток векторів а ⃗ і в ⃗ додатній

8. (2б.) З деякої точки проведено до площини дві похилі, проекції яких дорівнюють 4√3 см і 9 см. Знайдіть довжину більшої похилої, якщо менша похила утворює з площиною кут 60°.
9. (2б.) Знайдіть довжину діагоналі ВД паралелограмаа АВСД, якщо А(-1;-3;0), В(-1;1;3), С(3;1;4).
10.(3б.) Точка М рівіновіддалена від усіх сторін прямокутного трикутника і знаходиться на відстані 4см від його площини. Знайдіть відстань від точки М до сторін трикутника, якщо його гіпотенуза на 3см і 6см більша від катетів.

👇

Открыть все ответы

Ответ:

ТупенькийХлебушек1

06.12.2020

№1)Найти сумму первых членов геометрической прогрессии если:1)b1=5; g=-1; n=92) b1=2; g=2; n=53)b1=1/8; g=5; n=4
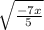
Sn=b1(1-q^n)/(1-q) если q<>1
b1- рервый член
q- коэффициент
1. Sn=5(1-(-1)^9)/(1-(-1))=5*2/2=5
2. Sn=2(1-2^5)/(1-2)=2*(-31)/(-1)=62
3. Sn=1/8(1-5^4)/(1-5)=1/8*(-624)/(-4)=39/2
№2) Найти сумму чисел если её слогаемые являются последовательными членами геометрической прогрессии 1/4+1/8+1/16++1/512
b1=1/4
q=1/2
bn=1/512
Sn=(bn*q-b1)/(q-1)=(1/512*1/2-1/4)/(1/2-1)=(-255/1024)/-1/2=255/512

4,6(2 оценок)

Ответ:

PicaChuShiK

06.12.2020

Объяснение:

выражение в квадратном корне должно давать положительный результат, иначе выражение не

имеет смысла

1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)

2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)

3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)

5) √25х. х должен быть 0 или положительное значение:

х≥0, поэтому х (0; +∞)

4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:

х (–∞; –1)

6) √0,01х, х≥0; х (0; +∞)

$\sqrt{ \frac{ - 7x}{5} }$

х ≥ 0; х (–∞; 0)

$\sqrt{81x {}^{2} }$

х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)

4,5(83 оценок)

Это интересно:

Транспорт

29.01.2021

Как правильно заботиться о мотоцикле и сделать его долговечным...

Дом-и-сад

08.01.2020

Как подготовить квартиру к отъезду: советы от профессионалов...

Здоровье

03.04.2021

Как вылечить прищемленный палец: лечение дома и медицинские советы...

Семейная-жизнь