Решите графическим систему уравнений :
1) {xy =2 , 2) { 2x² +2y = 10 ,
{x² -2y = -3 ; { - x +3y = 1 ;
ответ: 1) (1 ; 1/2)
2) (-7/3 ; -4/9) , (2 ;1)
Объяснение:
1) {xy =2 , {y =2/x || гипербола x =0 вертикальная асимптота
{x² -2y = -3 [ y =(1/2)x² + 3/2
2) ⇔ { y = - x²+5 , пока аналитическое решение
{ y =(1/3)x + 1/3
- x²+5 =(1/3)x +1/3 ⇔ 3x² -x -14 =0 D =(-1)² -4*(3)*(-14)= 169 =13²
⇒ x₁,₂ = (-1 ±13)/6
x₁ = (-1 -13)/(2*3) = -7/3 , y₁ =- x₁²+5 =(-7/3)²= -4/9 ;
x₂ = (-1 +13)/6 =2 , y₁ =(-7/3)x²₁+1/3 =(1/3)*(-7/3) +1/3=-4/3
ответ : ( -7/3 ; -4/9) и (2 ;1)

Определения к заданию
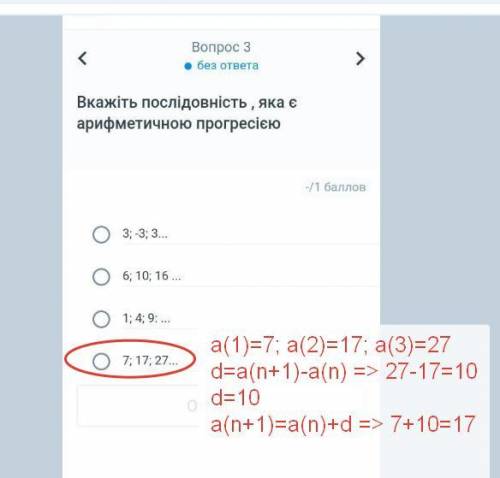
1 )Арифметическая прогрессия - это числовая последовательность, в которой каждый член, начиная со второго, равен сумме первого члена и разности d: a(n+1)=a(n)+d)
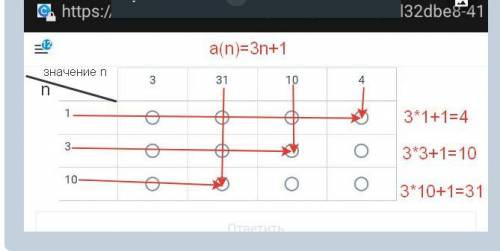
2) Арифметическая прогрессия может быть задана аналитическим При этом последовательность задается в виде формулы, и,подставляя в нее вместо переменной n, натуральные числа, возможно найти значение любого ее члена.
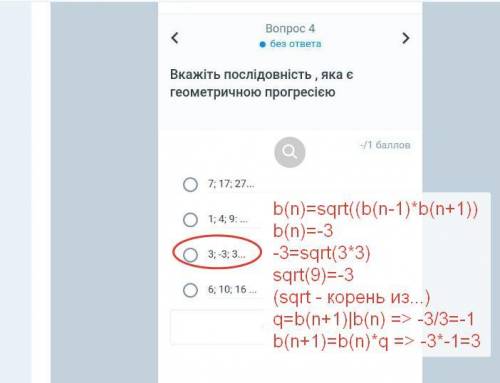
3) Чтобы определить является ли заданная последовательность геометрической прогрессией, можно воспользоваться формулой: b(n)=√(b(n-1))*b(n+1)) - значение члена геометрической прогрессии = корню из произведения предыдущего и последующего членов.
Решение во вложении
конкретней можеш написать я немону найти!!