В решении.
Объяснение:
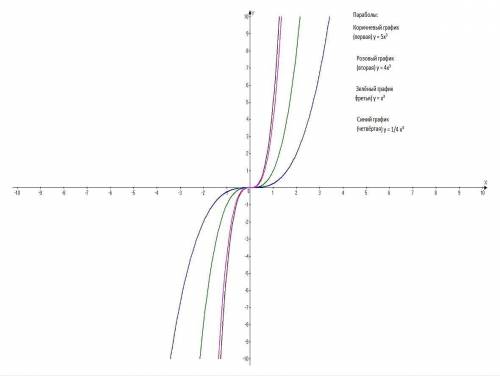
Построить в одной системе координат графики функций:
у = х³; у = 5х³; у = х³/4; у = 4х³.
Все графики - кубические параболы с вершиной в начале координат (0; 0). у = х³ - классическая парабола, остальные, в зависимости от коэффициента перед х³ "уже" или "шире" её.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
1) у = х³;
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
2) у = 5х³;
Таблица:
х -2 -1 0 1 2
у -40 -5 0 5 40
3) у = 1/4 х³ = х³/4;
Таблица:
х -3 -2 -1 0 1 2 3
у -6,75 -2 -0,25 0 0,25 2 6,75
4) у = 4х³;
Таблица:
х -2 -1 0 1 2
у -32 -4 0 4 32
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 83). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
83 = √а
(83)² = (√а)²
а=6889;
b) Если х∈[0; 36], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√36=6;
При х∈ [0; 36] у∈ [0; 6].
с) y∈ [14; 28]. Найдите значение аргумента.
14 = √х
(14)² = (√х)²
х=196;
28 = √х
(28)² = (√х)²
х=784;
При х∈ [196; 784] y∈ [14; 28].
d) Найдите при каких х выполняется неравенство у ≤ 5.
√х <= 5
(√х)² <= (5)²
х <= 25;
Неравенство у ≤ 5 выполняется при х <= 25.
Объяснение:
решение на фото