5 удачи ^-^ чтобы все было хорошо
ОДЗ первого неравенства находим из условия
х-2>0⇒x>2
x+2>0⇒x>-2
Значит, ОДЗ х>2, или х∈(2;+∞), а второго
(x-2)(x+x)>0 найдем решения методом интервалов.
х=2, х=-2,
-22
+ - +
х∈(-∞;-2)∪(2;+∞)
я ВЫДЕЛИЛ Вам жирным шрифтом ОДЗ, видите разницу? Так вот применение свойства
㏒ₐx+㏒ₐy=㏒ₐ(xy) расширяет область определения на интервал
(-∞;-2)
поэтому, решая первое неравенство системы, (x-3)*(x+3)>0
-33
+ - +
Вы получите лишний промежуток, а именно (-∞;-3), входящий в интервал (-∞;-2); его надо исключить из ответа.
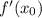производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.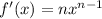
- где n это степень.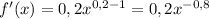
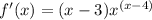
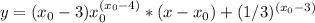
и получаешь уравнение касательной.
ответ:5
И так до бесконечнсти будет 4,5,4,5
Удачи закончить учебный год на отлично