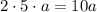
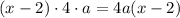

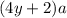 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: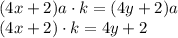
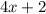 и выражение
и выражение 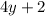 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном  возникает противоречие:
возникает противоречие:
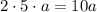
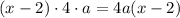

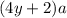 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: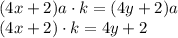
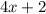 и выражение
и выражение 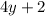 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном  возникает противоречие:
возникает противоречие:
Решение системы уравнений (-6; 12)
Объяснение:
Решить систему уравнений :
6x-y= -48
3x+6y=54
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
-у= -48-6х
у=48+6х
3x+6(48+6х)=54
3х+288+36х=54
39х=54-288
39х= -234
х= -234/39
х= -6
у=48+6х
у=48+6*(-6)
у=48-36
у=12
Решение системы уравнений (-6; 12)