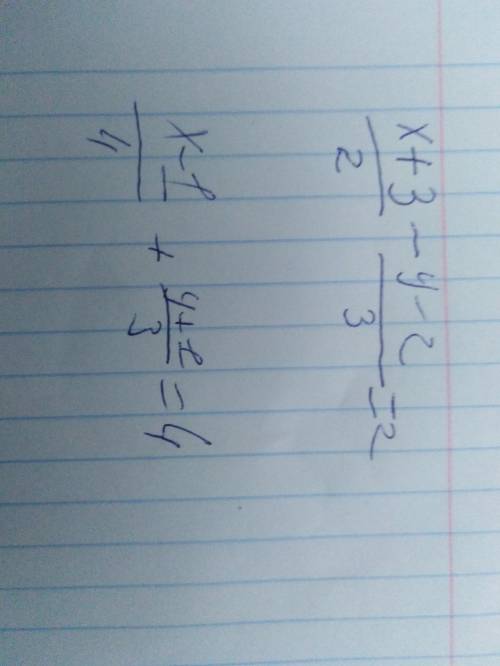
Объяснение:
В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны. Если в ромбе провести диагонали, то они разобьют ромб на 4 равных прямоугольных треугольника.
Тогда рассмотрим один из таких треугольников.
В нем известна сторона ромба- это будет гипотенуза для ∆, и один из катетов, это половина первой диагонали ромба, второй катет не известен, но он половина второй диагонали ромба.
По теореме Пифагора:
10²=(16/2) ²+х²
100=64²+х²
Х²=100-64=36; х=6 см, тогда вторая диагональ равна 6*2=12 см.
S=0,5*d1*d2=0,5*16*12=96 см²
Представьте многочлен в виде произведения:
Объяснение: (A±B)² =A² ± 2AB+B² ; A²- B² = (A - B)(A+B) .
а) 4a²-4ab + b² — 4 =(2a -b)² - 2² =(2a -b - 2)(2a -b + 2) ;
б) 9-25x²+ 30 ху-9y² =3² - (5x -3y)² = (3 - 5x +3y)(3 + 5x -3y) ;
в) 36x²-25+60xy +25y² =( 6 x+5y)²-(5)² = (6 x+5y -5) (6 x+5y+5) ;
г) 16-24ab-16a²-9b²=(4)²-(4a+3b)²=(4-4a-3b)(4+4a+3b) ;
е) 25a²-20a+4-4b²=(5a -2)²-(2b)² =(5a -2-2b)(5a -2+2b) ;
ж) 16c²-9m²-42m-49=(4c)² - (3m +7)² = (4c -3m -7)(4c +3m +7) ;
з) 70x+25-36y²+49x² = (5 +7x)² -(6y)²=(5 +7x -6y)(5 +7x +6y) ;
!!
д) 9n²- 16m²+40m-25 = (3n)² - (4m - 5)² =(3n - 4m+5)(3n +4m+5)