Точка движется прямолинейно по закону x(t)=3t^3+2t+1 найдите её ускорение в момент времени t=2с?

👇

Увидеть ответ

Ответ:

СВЕТЛАНУШЕНЬКА

26.01.2020

а=s''(t)

Скорость это первая производная от расстояния, сначала ищем её.

v= (3t³+2t+1)'= 9t²+2

a= (9t²+2)'=18t

a= 18·2=36 м/с²

4,5(91 оценок)

Открыть все ответы

Ответ:

PaulinaWalters

26.01.2020

Доказать тождество:

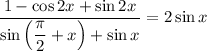
$\dfrac{1 - \cos 2x + \sin 2x}{\sin \left(\dfrac{\pi }{2} + x \right) + \sin x} = 2\sin x$

1. Определим область допустимых значений.

1.1. Выражение слева имеет смысл, если его знаменатель не равен нулю:

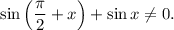
$\sin \left(\dfrac{\pi}{2} + x \right) + \sin x \neq 0.$

1.2. Используя формулу приведения 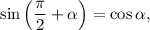$\sin \left(\dfrac{\pi}{2} + \alpha \right) = \cos \alpha,$ получаем:

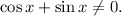
$\cos x + \sin x \neq 0.$

1.3. Умножим обе части на 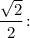$\dfrac{\sqrt{2} }{2} \colon$

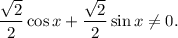
$\dfrac{\sqrt{2}}{2} \cos x + \dfrac{\sqrt{2}}{2} \sin x \neq 0.$

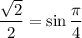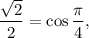1.4. Поскольку $\dfrac{\sqrt{2}}{2} = \sin \dfrac{\pi }{4}$ и $\dfrac{\sqrt{2}}{2} = \cos \dfrac{\pi }{4},$ то получаем:

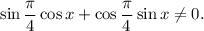
$\sin \dfrac{\pi}{4} \cos x + \cos \dfrac{\pi}{4} \sin x \neq 0.$

1.5. Используя формулу синуса суммы 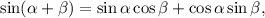$\sin (\alpha + \beta )=\sin \alpha \cos \beta + \cos\alpha \sin \beta,$ получаем:

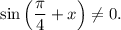
$\sin \left(\dfrac{\pi}{4} + x \right) \neq 0.$

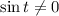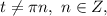1.6. Так как $\sin t \neq 0$ для $t \neq \pi n, ~ n \in Z,$ то:

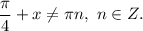
$\dfrac{\pi }{4} + x \neq \pi n, ~ n \in Z.$

1.7. Перенесём 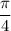$\dfrac{\pi}{4}$ в правую часть, изменив знак на противоположный:

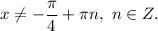
$x \neq -\dfrac{\pi }{4} + \pi n, ~ n \in Z.$

2. Докажем данное тождество, работая с левой частью равенства.

2.1. Преобразуем данное выражение, применив формулу косинуса двойного угла 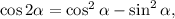$\cos 2\alpha = \cos^{2}\alpha - \sin^{2} \alpha,$ синуса двойного угла 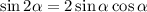$\sin 2\alpha = 2\sin \alpha \cos \alpha$ и формулу приведения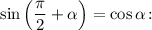 $\sin \left(\dfrac{\pi}{2} + \alpha \right) = \cos \alpha \colon$

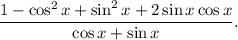
$\dfrac{1 - \cos^{2}x + \sin^{2}x + 2\sin x\cos x}{\cos x + \sin x}.$

2.2. Замечаем в числителе следствие из основного тригонометрического тождества 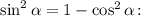$\sin^{2}\alpha = 1 - \cos^{2}\alpha \colon$

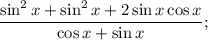
$\dfrac{\sin^{2}x + \sin^{2}x + 2\sin x\cos x}{\cos x + \sin x};$

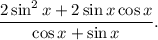
$\dfrac{2\sin^{2}x + 2\sin x\cos x}{\cos x + \sin x}.$

2.3. Вынесем в числителе общий множитель 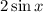$2\sin x$ за скобки:

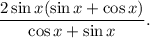
$\dfrac{2\sin x(\sin x + \cos x)}{\cos x + \sin x}.$

2.4. Сокращаем дробь на 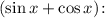$(\sin x + \cos x) \colon$

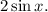
$2\sin x.$

Тождество доказано.

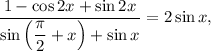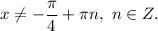
ответ: $\dfrac{1 - \cos 2x + \sin 2x}{\sin \left(\dfrac{\pi }{2} + x \right) + \sin x} = 2\sin x,$ если $x \neq -\dfrac{\pi }{4} + \pi n, ~ n \in Z.$

Пометка. Пункт под нахождением области допустимых значений не является обязательным при доказательстве тождества.

4,7(6 оценок)

Ответ:

Messidarcelona05

26.01.2020

В решении.

Объяснение:

Турист проплыл на байдарке 18 км по течению реки и 10 км против течения реки за тоже время, какое понадобилось ему, чтобы проплыть по озеру 28 км. С какой скоростью плыл турист по озеру, если скорость течения реки равно 2 км/ч?

Формула движения: S=v*t

S - расстояние v - скорость t – время

х - собственная скорость лодки (и скорость по озеру).

х + 2 - скорость лодки по течению.

х - 2 - скорость лодки против течения.

18/(х + 2) - время лодки по течению.

10/(х - 2) - время лодки против течения.

28/х - время лодки по озеру.

По условию задачи уравнение:

18/(х + 2) + 10/(х - 2) = 28/х

Умножить все части уравнения на х(х + 2)(х - 2), чтобы избавиться от дробного выражения:

18*х(х - 2) + 10*х(х + 2) = 28*(х + 2)(х - 2)