E(y)=[-4; 0]
Объяснение:
Нужно найти область значений, то есть E(y), функции у=х²-2·x-3 на промежутке [0;3].
Графиком функции является парабола, ветви которой направлены вверх. Определим абсциссу вершину параболы:
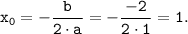
Так как x₀=1 ∈ [0; 3], то функция принимает наименьшее значение на этом промежутке:
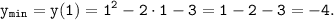
Далее, ветви параболы направлены вверх и поэтому наибольшее значение функция принимает на концах этого промежутка. Вычислим значение этой функции:
y(0)=0²-2·0-3= -3,
y(3)=3²-2·3-3= 0.
Отсюда, наибольшее значение функции
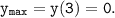
Значит, область значений функции на промежутке [0;3]: E(y)=[-4; 0].
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение: