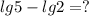
c=920
d=640
Объяснение:
Известно, что 30% числа c на 20 больше, чем 40% числа d,
а 30% числа d на 8 больше, чем 20% числа c.
Найти числа c и d.
Согласно условию задания составляем систему уравнений:
0,3c-0,4d=20
0,3d-0,2c=8
Выразим c через d в первом уравнении, подставим выражение во второе уравнение и вычислим d:
0,3c=20+0,4d
c=(20+0,4d)/0,3
0,3d-0,2[(20+0,4d)/0,3]=8
0,3d-[(4+0,08d)/0,3]=8
Умножим полученное уравнение на 0,3, избавимся от дроби:
0,09d-4-0,08d=2,4
0,01d=2,4+4
0,01d=6,4
d=6,4/0,01
d=640
c=(20+0,4d)/0,3
c=(20+0,4*640)/0,3
c=(20+256)/0,3
c=276/0,3
c=920
c=920
d=640
Объяснение:
Известно, что 30% числа c на 20 больше, чем 40% числа d,
а 30% числа d на 8 больше, чем 20% числа c.
Найти числа c и d.
Согласно условию задания составляем систему уравнений:
0,3c-0,4d=20
0,3d-0,2c=8
Выразим c через d в первом уравнении, подставим выражение во второе уравнение и вычислим d:
0,3c=20+0,4d
c=(20+0,4d)/0,3
0,3d-0,2[(20+0,4d)/0,3]=8
0,3d-[(4+0,08d)/0,3]=8
Умножим полученное уравнение на 0,3, избавимся от дроби:
0,09d-4-0,08d=2,4
0,01d=2,4+4
0,01d=6,4
d=6,4/0,01
d=640
c=(20+0,4d)/0,3
c=(20+0,4*640)/0,3
c=(20+256)/0,3
c=276/0,3
c=920
Объяснение:
1) lg5-lg2=lg2.5 ⇒
2)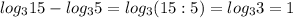
3) Решаем уравнение:
ответ: 2