Объяснение:
a) x² - 2x - 15 < 0
x² + 3x - 5x - 15 > 0
x(x + 3) - 5(x + 3) > 0
(x + 3)(x - 5) > 0
x + 3 < 0 x - 5 > 0
x < -3 x > 5
x ∈ (-∞, -3) ∪ (5, +∞)
б) -x² + 6x ≥ 0
-x(x - 6) ≥ 0
x(x - 6) ≤ 0
x ≥ 0 x - 6 ≤ 0
x ≤ 6
x ∈ [0, 6]
в) 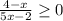
4 - x ≤ 0 5x - 2 > 0
x ≤ 4 5x > 2
x > 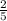
x ∈ (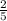 , 4]
, 4]
г) x(x - 9)(x + 2) > 0
x < 0 (x - 9)(x + 2) > 0
x - 9 > 0 x + 2 > 0
x > 9 x > -2
x ∈ (-2, 0) ∪ (9, +∞)
д) 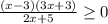
2x + 5 > 0 (x - 3)(3x + 3) ≥ 0
2x > -5 x - 3 ≥ 0 3x + 3 ≤ 0
x > 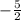 x ≥ 3 3x ≤ -3
x ≥ 3 3x ≤ -3
x ≤ -1
x ∈ (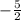 , -1] ∪[3, +∞)
, -1] ∪[3, +∞)
Объяснение:
А. 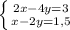
Чтобы сложить эти уравнения. нужно домножить второе уравнение на -2, получим систему
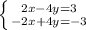
-2х и 2х равны 0, -4y и 4y равны 0, 3 и -3 тоже равны 0, получаем
0=0
Это значит, что система имеет множество решений.
Б. 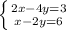
Домножим второе уравнение на -2
Получим систему
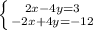
При сложении получаем
0=-9
Значит, система не имеет решений.
В. 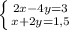
Домножим второе уравнение на -2
Получим систему
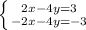
При сложении получим
-8y=0
y=0
Подставим в первое уравнение и получим
2x -4*0=3
2x=3
x=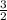
Значит, система имеет одно решение и оно нам не подходит.
Г. 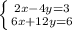
Домножим первое уравнение на -3 и получим систему
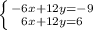
При сложении получим
24y=-3
y=-3: 24
y= 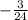
y= 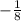
При подстановке в первое уравнение получим
2x - 4 * (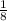 ) = 3
) = 3
2x = 3 * 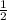
2x=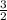
x= 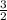 : 2
: 2
Двойка сокращается и получается
x=3
Значит система имеет одно решение и оно нам тоже не подходит.
ответ. А
B - студент выучил по другому предмету 16 вопросов из 20
Вероятность того, что студент получит зачет по одному предмету: P(A)=18/25
Вероятность того, что студент получит зачет по другому предмету: P(B)=16/20
Поскольку события A,B - независимы, то искомая вероятность равна P = P(A)*P(B) = 18/25 * 16/20 ≈ 0.576 - ОТВЕТ.