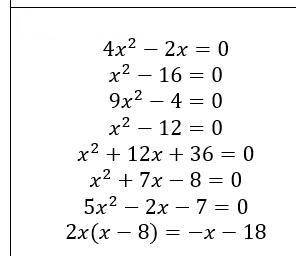
Объяснение:
1. Всего 6 вероятных событий
1) 1 исход нас устраивает. P(двойки)=1/6
2) 2 благоприятных исхода. P(4 и 6) = 2/6 = 1/3
3) 2 благоприятных исхода. P(1 и 2)=2/6=1/3
4) 3 благоприятных исхода (1,3,5). P(нечетное)=3/6=1/2
2. 2 белых + 5 красных.
а) белый - всего 7 шаров, 2 исхода благоприятные P(белый)=2/7
б) красный - всего 7 шаров, 5 исходов благоприятные Р(красный)=5/7
в)зеленый - вероятность 0.
3. 3 красных + 9 синих
а)Т.к. они все не белые, то 1 или 100%
б) красный - всего 12 шаров, 3 благоприятных исхода P(красный)=3/12=1/4
в) синий - всего 12 шаров, 9 благоприятных исходов Р(синий)=9/12=3/4
Объяснение:
Линейное уравнение – уравнение, сводящееся к виду ax+b=0, где a≠0,b – числа. Линейное уравнение всегда имеет единственное решение x=−ba. Квадратное уравнение – уравнение, сводящееся к виду ax2+bx+c=0, где a≠0,b,c – числа. Выражение D=b2−4ac называется дискриминантом квадратного уравнения. Квадратное уравнение может иметь не более двух корней: ∙ если D>0, то оно имеет два различных корня и x1=−b+D2aиx2=−b−D2a ∙ если D=0, то оно имеет один корень (иногда говорят, что два совпадающих) x1=x2=−b2a ∙ если D<0, то оно не имеет корней. ▸ Теорема Виета для квадратного уравнения: Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения x1+x2=−ba а произведение x1⋅x2=ca ▸ Если квадратное уравнение: ∼ имеет два корня x1 и x2, то ax2+bx+c=a(x−x1)(x−x2). ∼ имеет один корень x1 (иногда говорят, что два совпадающих), то ax2+bx+c=a(x−x1)2. ∼ не имеет корней, то квадратный трехчлен ax2+bc+c никогда не может быть равен нулю. Более того, он при всех x строго одного знака: либо положителен, либо отрицателен. ▸ Полезные формулы сокращенного умножения: x2−y2=(x−y)(x+y)(x+y)2=x2+2xy+y2(x−y)2=x2−2xy+y2 Ознакомиться с полной теорией
Объяснение:
1) 4х²-2х=0
2х(2х-1)=0
2х=0⇒х=0
2х-1=0⇒2х=1⇒х=0,5
ответ: 0; 0,5;
х²-16=0⇒х²=16⇒х=±√16⇒х=±4
ответ: -4;4;
3) 9х²-4=0⇒ 9х²=4⇒х²=4/9⇒х=±√4/9⇒х=±2/3
ответ: -2/3; 2/3;
4)х²-12=0
х²=12⇒х=±√12⇒х=±2√3
ответ: -2√3;2√3
5)х²+12х+36=0
(х+6)²=0⇒х+6=0⇒х=-6
ответ: -6;
6)х²+7х-8=0
По теореме, обратной теореме Виета х1+х2=-7;х1·х2=-8 Отсюда, х1=-8;х2=1
ответ: -8;1;
5х²-2х-7=0
D=(-2)²-4·5·(-7)=4+140=144;√D=√144=12;
х=(2±12)/2·5=(2±12)/10
х1=(2-12)/10=-10/10=-1
х2=(2+12)/10=14/10=7/5=1,4
ответ:-1;1,4;
7)2х(х-8)=-х-18
2х²-16х=-х-18
2х²-15х+18=0
D=(-15)²-4·2·18=225-144=81; √D=√81=9
х=(15±9)/2·2=(15±9)/4
х1=(15-9)/4=6/4=1,5
х2=(15+9)/4=24/4=6
ответ:1,5; 6;