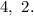Поскольку эта задача уже решалась совсем недавно, позволю себе опустить подробности. Дважды возводя в квадрат (второй раз - уединяя корень), получим уравнение
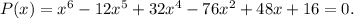
Сначала будем искать так называемые парные корни, то есть корни вида  Такие корни ходят парами, дают в разложении скобку (x²-a^2). Для поиска таких корней надо решать систему из двух уравнений, приравнивая отдельно к нулю сумму четных степеней и сумму нечетных степеней. Доказательство этого факта я оставляю читателю. В нашем случае находим корни
Такие корни ходят парами, дают в разложении скобку (x²-a^2). Для поиска таких корней надо решать систему из двух уравнений, приравнивая отдельно к нулю сумму четных степеней и сумму нечетных степеней. Доказательство этого факта я оставляю читателю. В нашем случае находим корни 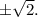 Далее ищем кратные корни (они, как известно, ищутся из системы
Далее ищем кратные корни (они, как известно, ищутся из системы 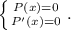 В результате находится кратный корень 2 кратности 2. После деления остается квадратный трехчлен с конями
В результате находится кратный корень 2 кратности 2. После деления остается квадратный трехчлен с конями 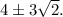 Работу по выделению истинных корней оставляю читателю. ответ:
Работу по выделению истинных корней оставляю читателю. ответ: 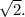
На этом разрешите закончить это немного хулиганское решение.
Если кто-нибудь захочет услышать поподробнее про парные корни, составьте самостоятельно многочлен с парными корнями, приравняйте его к нулю и предложите мне решить такое уравнение. В этом случае я все внимание уделю этой теме.
Задача. Сколько действительных корней имеет уравнение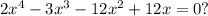
Укажите интервал, которому принадлежит наименьший корень:
ответ запишите в виде: где
где 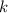 — число корней,
— число корней, 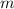 — номер промежутка, которому принадлежит наименьший корень.
— номер промежутка, которому принадлежит наименьший корень.
Решение. Вынесем общий множитель за скобки:
за скобки:
Произведение множителей равно нулю тогда, когда хотя бы один из них равен нулю:
Видя последнее уравнение, понимаем, что искать все его корни не нужно. Этого и не требуют в задании.
Рассмотрим функцию
1) Область определения:
2) Исследуем данную функцию на четность:
Функция не обладает свойством четности. Она ни четная, ни нечетная.
3) Определим нули функции.
3.1. Пересечение с осью
Невозможно дать точный ответ.
3.2. Пересечение с осью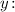
Значит, — точка пересечения с осью
— точка пересечения с осью 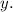
4) Найдем производную функции:
5) Определим критические точки функции, приравняв производную к нулю:
Определим точки экстремума и экстремумы функции:
Итак:
6) Изобразим схематически график функции, строго соблюдая все найденные точки, монотонность функции и симметрию линий около критических точек (см. вложение).
Выводы. Как видно из графика, из уравнения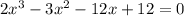 имеем три действительных корня, наименьший из которых находится в интервале
имеем три действительных корня, наименьший из которых находится в интервале 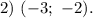 Таким образом, уравнение
Таким образом, уравнение 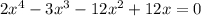 имеет четыре действительных корня.
имеет четыре действительных корня.
ответ: