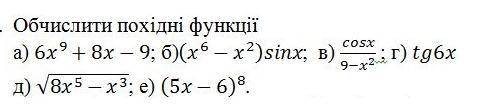
Чтобы найти значение выражения а * ( а + b ) ^ 2 + 2 * a * ( a ^ 2 + b ^ 2 ) - a * ( a - b ) ^ 2 при а = 2 , 5 и b = 0 , 5, надо выражение сначала упростить, потом известные значения подставить в само выражение. То есть получаем:
а * ( а + b ) ^ 2 + 2 * a * ( a ^ 2 + b ^ 2 ) - a * ( a - b ) ^ 2 = a * ( a ^ 2 + 2 * a * b + b ^ 2 ) + 2 * a ^ 3 + 2 * a * b ^ 2 - a * ( a ^ 2 - 2 * a * b + b ^ 2 ) = a ^ 3 + 2 * a ^ 2 * b + a * b ^ 2 + 2 * a ^ 3 + 2 * a * b ^ 2 - a ^ 3 + 2 * a ^ 2 * b - b ^ 2 * a = 4 * a ^ 2 * b + 2 * a ^ 3 + 2 * a * b ^ 2 = 4 * 2 . 5 ^ 2 * 0 . 5 + 2 * 2 . 5 ^ 3 + 2 * 2 . 5 * 0 . 5 ^ 2 = 12 . 5 + 31.25 + 1.25 = 45.
Объяснение:
а) f'(x)= 54x⁸+8
б) f'(x)= (x⁶-x²)'sin(x)+(x⁶-x²)*(sin(x))'= sin(x)*(6x⁵-2x)+cos(x)(x⁶-x²)= sin(x)*2x(3x⁴-1)+cos(x)*x²(x⁴-1)
в) f'(x)= (cos(x)'(9-x²)-cos(x)*(9-x²)')/(9-x²)²= (-sin(x)(9-x²)+cos(x)*2x)/(9-x²)²
г) f'(x)= 6/cos²(6x)
д) f'(x)= 1/2√8x⁵-x³ * (40x⁴-3x²)= (40x⁴-3x²)/2√8x⁵-x³
е) f'(x)= 8(5x-6)⁷*5= 40(5x-6)⁷