Алгебра: Знайдіть похідну функції f(x) =x³+½x²-x+5. В точці 2.

Знайдіть похідну функції f(x) =x³+½x²-x+5. В точці 2.

👇

Увидеть ответ

Ответ:

verik2643

02.03.2023

вавачаві

Объяснение:

врнре

4,5(4 оценок)

Открыть все ответы

Ответ:

жансая87

02.03.2023

1. 6sin²x - 7sinx - 5 = 0

t = sinx: [-1;1]

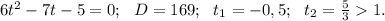
$6t^2-7t-5=0;\ \ D=169;\ \ t_1=-0,5;\ \ t_2=\frac{5}{3}1.$

sinx=-0,5.

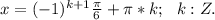
$x=(-1)^{k+1}\frac{\pi}{6}+\pi*k;\ \ k:Z.$

2. 3sin²x + 10 cosx - 10 = 0

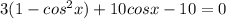
3(1-cos^2x)+10cosx-10=0

$3cos^2x-10cosx+7=0;\ \ cosx=t:\ [-1;1].$

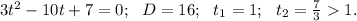
$3t^2-10t+7=0;\ \ D=16;\ \ t_1=1;\ \ t_2=\frac{7}{3}1.$

cosx=1

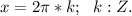
$x=2\pi*k;\ \ k:Z.$

3. 2sin²x + 11sinx*cosx + 14cos²x = 0

Поделим данное однородное уравнение на квадрат косинуса и сделаем замену переменной: tgx=t

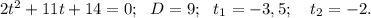
$2t^2+11t+14=0;\ \ D=9;\ \ t_1=-3,5;\ \ \ t_2=-2.$

tgx=-2 tgx=-3,5

Имеем две группы углов:

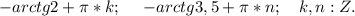
$-arctg2+\pi*k;\ \ \ \ -arctg3,5+\pi*n;\ \ \ k,n:Z.$

4. 3tg x - 5ctg x + 14 = 0

Пусть tgx=t

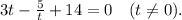
$3t-\frac{5}{t}+14=0\ \ \ (t\neq0).$

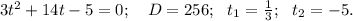
$3t^2+14t-5=0;\ \ \ D=256;\ \ t_1=\frac{1}{3};\ \ t_2=-5.$

В ответе имеем две группы углов:

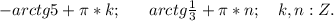
$-arctg5+\pi*k;\ \ \ \ \ arctg\frac{1}{3}+\pi*n;\ \ \ k,n:Z.$

5. 10sin²x - sin2x = 8cos²x

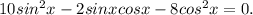
10sin^2x-2sinxcosx-8cos^2x=0.

Аналогично задаче 4, сделаем замену переменной tgx=t после деления на квадрат косинуса и сокращения на 2:

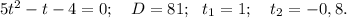
$5t^2-t-4=0;\ \ \ D=81;\ \ t_1=1;\ \ \ t_2=-0,8.$

В ответе имеем две группы углов:

$-arctg0,8+\pi*k;\ \ \ \ \ \frac{\pi}{4}+\pi*n;\ \ \ k,n:Z.$

6. 1 - 6cos²x = 2sin2x + cos2x

Применив основное тождество и формулы синуса и косинуса двойного угла, получим:

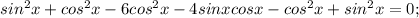
sin^2x+cos^2x-6cos^2x-4sinxcosx-cos^2x+sin^2x=0;

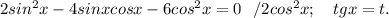
$2sin^2x-4sinxcosx-6cos^2x=0\ \ /2cos^2x;\ \ \ tgx=t.$

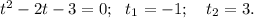
$t^2-2t-3=0;\ \ t_1=-1;\ \ \ t_2=3.$

В ответе имеем две группы углов:

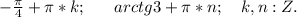
$-\frac{\pi}{4}+\pi*k;\ \ \ \ \ arctg3+\pi*n;\ \ \ k,n:Z.$

4,8(72 оценок)

Ответ:

VodDamirVod

02.03.2023

Задача на нахождение расстояния, скорости, времени
S(расстояние)=v(скорость)×t(время)
Условия:
S(по теч.) = 115 км
S(пр.теч.)=170 км
t(пр. теч.) - t(по теч.)=5 ч
v(соб.)=20 км/ч
Найти:
v(теч.)-? км/ч
Решение
Пусть х км/ч - скорость течения реки.
Скорость катера по течению реки равна v(по теч.) = v(соб.) + v(теч.) = 20+х км/ч
Скорость катера против течения реки равна v(пр. теч.) = v(соб.) - v(теч.) = 20-х км/ч
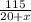По течению реки катер проплыл 115 км и затратил: t(по теч.)= $\frac{115}{20+x}$ часов.
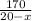Против течения катер проплыл 170 км и затратил t(пр. теч.)= $\frac{170}{20-x}$ часов.
t(пр. теч.) - t(по теч.)=5 часов
Составим и решим уравнение:
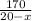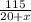$\frac{170}{20-x}$ - $\frac{115}{20+x}$ = 5 (умножим все на (20+х)(20-х), чтобы избавиться от дробей)

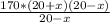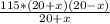$\frac{170*(20+x)(20-x)}{20-x}$ - $\frac{115*(20+x)(20-x)}{20+x}$ = 5 (20+x)(20-x)
170×(20+х) - 115×(20-х) = 5×(400-х²)
170×(20+х) - 115×(20-х)=5×(400-х²)
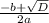3400+170х - 2300+115х=2000 - 5х²
1100+285х-2000+5х²=0
5х²+285х-900=0 (сократим на 5)
х²+57х-180=0
D=b²-4ac=57² - 4*1*(-180) = 3249 + 720=3969 (√3969=63)
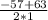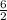х₁ = $\frac{-b+ \sqrt{D} }{2a}$ = $\frac{-57+63}{2*1}$ = $\frac{6}{2}$ = 3
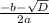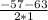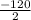x₂= $\frac{-b- \sqrt{D} }{2a}$ = $\frac{-57-63}{2*1}$ = $\frac{-120}{2}$ = -60 х<0 - не подходит.
х=3, скорость течения реки равна 3 км/ч
ответ: скорость течения реки равна 3 км/ч

4,6(45 оценок)

Это интересно:

Дом-и-сад

08.01.2020

Как подготовить квартиру к отъезду: советы от профессионалов...

Здоровье

03.04.2021

Как вылечить прищемленный палец: лечение дома и медицинские советы...

Семейная-жизнь

28.05.2021

Как помочь родителям, которые похоронили своего ребенка: советы и рекомендации...

Компьютеры-и-электроника