Корней нет
Объяснение:
Пусть х^2=t, следовательно
t^2+10t+9=0
По т. Виетта
t1+t2=-10
t1*t2=9. ; следовательно t1=-9 t2=-1
ООЗ:
t=x^2
-9=x^2
Нет корней
-1=х^2
Нет корней
ответ:корней нет
Объяснение:
(х+4)(х+3)(х+2)(х+1)-120=0 ;
групуємо множники так :
[(х+4)(х+1)] [(х+3)(х+2)] - 120 = 0 ;
( x² + 5x + 4 )( x² + 5x + 6 ) - 120 = 0 ;
позначимо x² + 5x + 4 = у , тоді
у * ( у + 2 ) - 120 = 0 ;
y² + 2y - 120 = 0 ; D = 484 > 0 ; y₁ = - 12 ; y₂ = 10 .
Маємо два простих рівняння :
x² + 5x + 4 = - 12 ; x² + 5x + 4 = 10 ;
x² + 5x + 16 = 0 ; x² + 5x - 6 = 0 ;
D = - 39 < 0 ; D = 49 > 0 ;
xЄ ∅ ; x₁ = - 6 ; x₂ = 1 .
В - дь : - 6 і 1 .
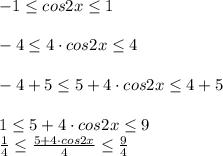
![[ \frac{1}{4};2 \frac{1}{4}]](/tpl/images/0413/8761/f42ca.png)
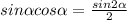
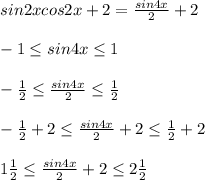
![[1 \frac{1}{2};2 \frac{1}{2}]](/tpl/images/0413/8761/944ce.png)
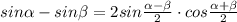
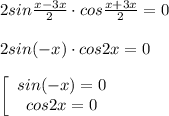
Объяснение:
x⁴+10x²+9=0
х²=t
t²+10t+9=0
t₁+t₂= -10
t₁t₂= 9
t₁= -9
t₂ = -1
x²≠ -9
x²≠ -1
корней нет