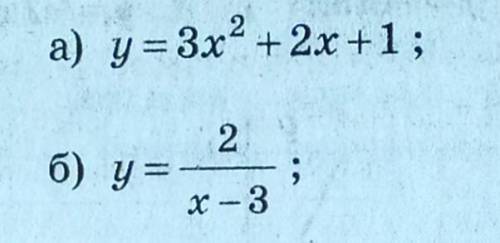
а) Х Є R , х - будь яке число
б) знаменник не має бути рівний нулю тому число 3 виключаємо з області визначення
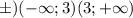
Для начала выразим в данном уравнении одну переменную через другую. Например, переменную 
через переменную 
.
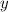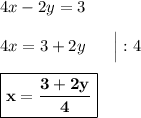
Для каждой пары решений этого уравнения данное равенство будет выполняться. Теперь берём для переменной 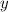любое значение, которое захотим, подставляем в выражение сверху и находим переменную . Возьмём, например,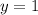 
, получится:
.
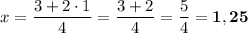Таким образом, пара чисел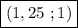 
является решением нашего уравнения. Подставим, например, 
:
.
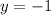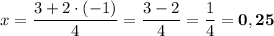И ещё одну пару чисел,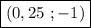 
, мы получили. И для последней пары мы возьмём, к примеру, 
:
.
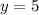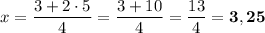И получили последнюю пару чисел: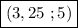 
.
Объяснение:
а) ОДЗ: х Є R (икс є будь-яке число)
б) ОДЗ: х-3≠0; х≠3; (-∞;3)U(3;∞)