Нам надо раскрыть три модуля, следовательно будем брать промежутки, на которых выражения, стоящие под модулями, будут менять знак. Чтобы узнать эти точки, надо приравнять нулю выражения, стоящие под модулями. Получаются точки x=1, x=2, x=3
Рассмотрим первый случай x<1
Раскрываем модули:
1-x+2-x+3-x=2
6-3x=2
3x=4
x=4/3
Найденное значение не принадлежит рассматриваемому промежутку. Решений нет.
Рассмотрим второй промежуток 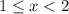
Раскрываем модули
x-1+2-x+3-x=2
4-x=2
x=2
Найденное значение не принадлежит рассматриваемому промежутку. Решений нет.
Рассматриваем третий промежуток 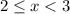
Раскрываем модули
x-1+x-2+3-x=2
x=2
Рассматриваем четвертый промежуток 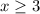
Раскрываем модули
x-1+x-2+x-3=2
3x-6=2
3x=8
x=8/3=2 2/3
Найденное значение не принадлежит рассматриваемому промежутку. Решений нет.
ответ: x=2.
Где
1)
Поначалу у функции
Это степенная функция, а производная любой степенной функции находится следующей формулой:
В нашем случае:
Так, нашли производную общего случая.
Так как, точки касания не даны, мы запишем нахождение касательной в любой точке этой функции:
2)
Опять же, найдем производную
Так как, точки касания не даны, мы запишем нахождение касательной в любой точке этой функции:
То есть, берешь любой икс, и вставляешь в выражение касательной вместо
Это и есть окончательные ответы.
Если что-то не правильно, то это значит что вы не правильно написали условие.