Экстремум - максимальное или минимальное значение функции. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум - точка экстремума называется точкой минимума, а если максимум — точкой максимума.
А теперь решение:
1)
необходимое условие экстремума функции одной переменной- в этой точке первая производная функции должна обращаться в нуль.
Найдем производную
приравняем ее к нулю
у нас две точки экстремума. Определим теперь какие это точки (максимума или минимума)
- Точка x₀ называется точкой максимума, если существует её окрестность, такая, что для всех значений данной окрестности выполнено неравенство: f(x)≤f(x₀) - Точка x₀ называется точкой минимума, если существует её окрестность, такая, что для всех значений данной окрестности выполнено неравенство: f(x)≥f(x₀)
Как это выглядит на решении?
нарисуем числовую прямую и отметим на ней точки- экстремумы и проверим знак производной на полученных интервалах:
+ - + ------- 0 ------------ 4 -----------
Значит на промежутке (-оо;0) функция возрастает на промежутке (0;4) - убывает на промежутке (4;+оо) - возрастает
Значит х=0 точка максимума значит х=4 точка минимума
Значение функции в точке х=0 - максимальное значение
значение функции в точке х=4 -минимальное значение
Далее решает по аналогии
2)
найдем точки экстремума
+ - + ----- 0 --------- 3 ------------ на промежутке (-оо;0) и (3;+оо) - возрастает на промежутке (0;3) убывает
х=0 точка максимума максимальное значение функции х=3 точка минимума минимальное значение функции
3)
+ - + ------ - 3 ------- 1 ----------
на промежутке (-00;-3) и (1;+оо) возрастает на промежутке (-3;1) убывает
х= -3 точка максимума минимальное значение
x=1 точка минимума минимальное значение
4)
+ - + ------- - 2 -------- 5 -------- на промежутке (-оо;-2) и (5;+оо) возрастает на промежутке (-2;5) убывает
точка х=-2 точка максимума максимальное значение
точка х=5 точка минимума минимальное значение
5)
- + -------------- 0 ---------------- на промежутке (-оо;0) убывает на промежутке (0;+оо) возрастает
Сначала разделим левую и правую часть уравнения на x, получим:
Решим сначала однородное уравнение, вида:
Это уравнение с разделяющимися переменными, получаем: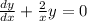
Берем интеграл от обоих частей получаем:
Дальше методом вариации свободной постоянной ищем частное решение неоднородного уравнения:
Представляем C как функцию от х, т.е C=C(x) и подставляем выражение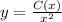 в исходное уравнение. Получаем:
в исходное уравнение. Получаем:
Сокращаем подобные и прочее, получаем:
Подставляем получившееся значение C(x) в выражение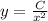 и получаем частное решение
и получаем частное решение 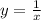
В итоге общее решение неоднородного уравнения это сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Т.е.
Все, уравнение решено. Теперь решаем задачу Коши:
Т.к.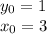
то приходим к уравнению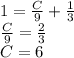
Все, нашли С, теперь пишем решение задачи Коши:
ответ: Общее решение дифференциального уравнения:
Частное решение дифференциального уравнения, удовлетворяющиего начальному условию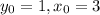 :
: