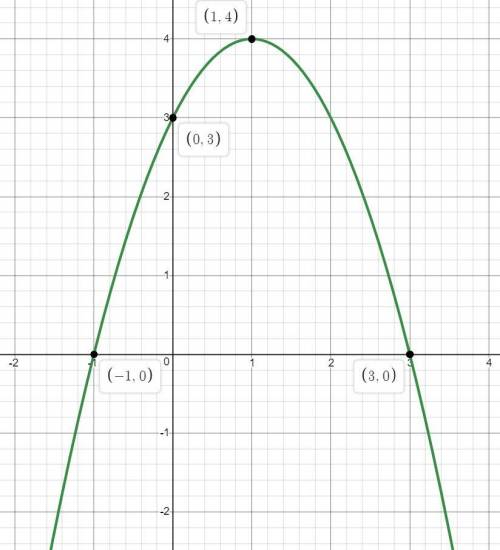
Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
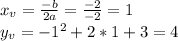
Это координаты вершины, почему именно такие? Корни уравнения:
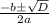, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.
Найдём нули функции:
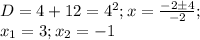
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: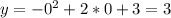 
то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)
Этот промежуток имеет соответствующие неравенства x < a x a x>a, где a a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a a - ( x < a ) (x a ) (x>a). Множество чисел, которые будут удовлетворять неравенству вида x < a x a x>a, как ( a , + ∞ ) (a, +∞). Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x < a x a x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при штриховки. Рассмотрим рисунк, приведенный ниже. Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Объяснение:
надеюсь правильно ))