Для решения этой задачи используем формулы арифметической прогрессии.
а₁=5 [в первый день 5 капель]
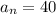 [день, в который нужно выпить 40 капель]
[день, в который нужно выпить 40 капель]
d=5 [разность арифметической прогрессии, т.к. каждый день дозировка увеличивается на одну и ту же величину - 5 капель]
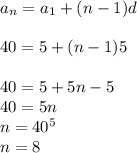
На восьмой день дозировка составит 40 капель.
По формуле суммы n первых членов арифметической прогрессии найдм сколько всего капель нужно выпить больному за 8 дней.
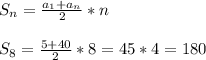
180 капель должен выпить больной за первые 8 дней лечения.
В последний период лечения больной должен уменьшать дозировку каждый день на 5 капель, и с дозировки в 40 капель дойти до 5 капель.
На это ему понадобиться 8 дней (также, как и в первый период лечения).
Суммарное количество капель, которые должен выпить больной за эти 8 дней, составит 180.
В середине лечения больной должен три дня подряд пить по 40 капель. Два раза по 40 капель мы уже учли. Поэтому к общей сумме добавим только 40.
180+180+40 = 400 (капель) - должен выпить больной за весь период лечения.
В одном пузырьке содержится 200 капель лекарства. Значит больному нужно купить 400:200 = 2 пузырька лекарства.
ответ: 2 пузырька.
x принадлежит [-1,1]
Объяснение:
-x^2+4-3>=0
-x^2+1>=0
Перенесём постоянную в правую часть и сменим её знак:
-x^2+1-1>=0-1
Сократим противоположные выражения:
-x^2>0-1
-x^2>=-1
Сменим знаки обеих частей неравенства и поменяем знак неравенства на противоположный:
-1x*(-x^2)<=-1x*(-1)
x^2<=-1*(-1)
x^2<=1
Извлечём √ из обеих частей неравенства:
√x^2<=√1
Сократим степень корня и показатель степени на 2:
(x)<=√1
Разделим неравенство на 2 возможных случая :
x<=1,x<=0
-x<=1,x<0
Найдём пересечение :
x принадлежит [0,1]
-x<=1,x<0
Решим уравнение относительно х:
-x<=1
Умножим обе части неравенства на -1 и перевернём знак неравенства :
-1*(-x)>=-1*1
x>=-1*1
x>=-1
Найдём пересечение : x принадлежит [0,1]
x принадлежит [-1,0]
Найдём объединение :
x принадлежит [-1,1]
x принадлежит [-1,1]