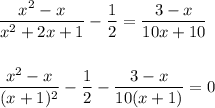
Теперь приводим дроби к одному знаменателю, который в данном случае будет равен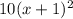 
. Для этого первую дробь мы домножаем на 10, вторую дробь - на 
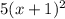, а третью - на 
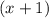. Получаем:
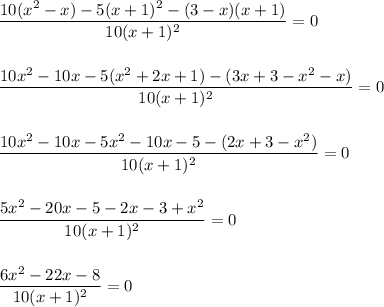
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
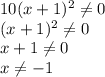
Приравняем числитель к нулю с учётом нашего условия:
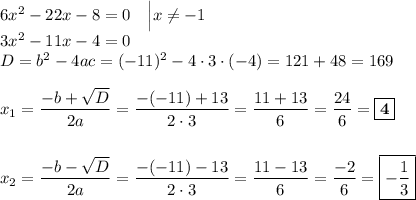
Таким образом, наше уравнение имеет два решения. Но по условию нас просят отобрать только целые решения. Наш первый корень, 4, принадлежит множеству целых чисел, в то время, как второй корень,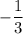 
, целым числом не является. Таким образом, в ответ пойдёт только 
.
ответ: 4.
a^2 - 36b^2 1 1
: ( - )
6ab 6b a
Сначала разберёмся с выражением в скобках, а конкретно, приведём к общему знаменателю дроби:
1 1 a - 6b
- --- =
6b a 6ab
Т.к. происходит деление на получившуюся дробь, то мы её переворачиваем и вместо деления ставим знак умножения:
a^2 - 36b^2 6ab a^2 - 36b^2 (a - 6b)*(a + 6b)
* = = = a + 6b
6ab a - 6b a - 6b a - 6b
Получившуюся в числителе разность квадратов, мы разложили на множители, после чего сократили.
Теперь можно подставлять конкретные значения:
a + 6b = 5 2/17 + 6 * (5 2/17) = (5 2/17) * (1 + 6) = (5 2/17) * 7
Смешанную дробь вынесли за скобки, в скобках получилось 7.
Превращаем смешанную дробь в неправильную:
5*17 + 2 87
5 2/17 = =
17 17
Умножаем неправильную дробь на 7:
87 609 14
* 7 = = 35 ≈ 38.82
17 17 17