ответ:1) Задание
Дана функция
найти промежутки возрастания и убывания
По признаку возрастания и убывания функции на интервале:
если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Найдем производную данной функции
найдем точки экстремума, точки в которых производная равна нулю
отметим точки на числовой прямой и проверим знак производной на промежутках
___+-+__
0 2
Значит на промежутках (-оо;0) ∪ (2;+оо) функция возрастает
на промежутке (0;2) функция убывает
точки х=0 точка минимума, х=2 точка максимума
Найти наибольшее и наименьшее значение функции на отрезке [-2; 1].
Заметим, что х=2 точка максимума не входит в данный промежуток,
а х=0 принадлежит данному промежутку
Проверим значение функции в точке х=0 и на концах отрезка
Значит наибольшее значение функции на отрезке [-2;1]
в точке х=0 и у(0)=1
значит наименьшее значение функции на отрезке [-2;1]
в точке х=-2 и у(-2)= -19
2. Напишите уравнение к касательной к графику функции
f(x)=x^3-3x^2+2x+4 в точке с абсциссой x0=1.
Уравнение касательной имеет вид
найдем производную данной функции
найдем значение функции и производной в точке х=1
подставим значения в уравнение касательной
Объяснение:
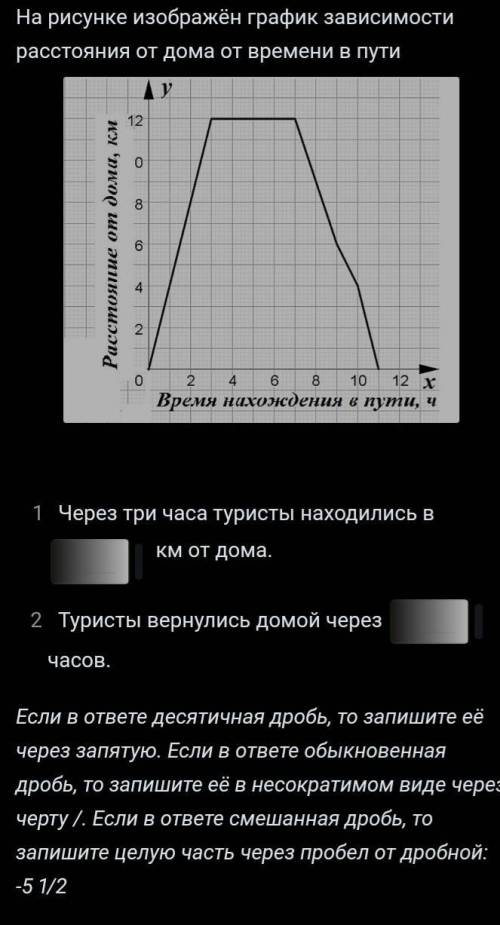
1)Через 3 часа туристы находились в 12 км от дома.
2)Туристы вернулись домой через 11 часов.
Объяснение:
1) Через 3 часа туристы находились в 12 км от дома.
(От точки 3 часа на горизонтальной прямой поднимаем перпендикуляр вверх, упираемся в точку на второй горизонтальной прямой, проводим мысленно прямую влево, и получаем отметку 12 км.)
2)Туристы вернулись домой через 11 часов.
(Здесь просто: вышли из дома на точке ноль часов, вернулись на точке 11 часов , между 10 и 12)