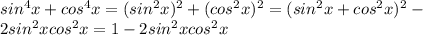
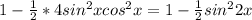
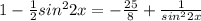
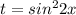 и продолжать решение уже дробно-рационального уравнения.
и продолжать решение уже дробно-рационального уравнения.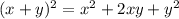
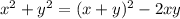
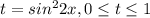
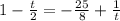
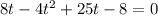
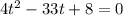
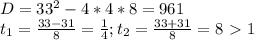 - этот корень не удовлетворяет нашему уравнению.
- этот корень не удовлетворяет нашему уравнению.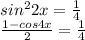
Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
Объяснение:
log₂(x²-5)*log₃²(7-x)+3log₂(x²-5)-2log₃²(7-x)-6=0
для упрщения записи сделаем замену:
log₂(x²-5)=y; y∈R
log₃²(7-x)=z; z∈R
тогда:
yz+3y-2z-6=o;
y(z+3)-(2z+6)=0;
y(z+3)-2(z+3)=0;
(z+3)(y-2)=0;
z+3=0; y-2=0;
z=-3; y=2.
log₂(x²-5)=2;
(x²-5)=2²;
x²-5-4=0;
x²=9; x=±3;
log₃²(7-x)=-3;
log₃(7-x)=√(-3) - решений в множестве R нет!
x=∅
x∈{-3;3}
lg²x+2log₁₀₀x-6=0; logₐb=logₓb/logₓa;
lg²x+ 2lgx/2-6=0; log₁₀₀x=lgx/lg100=lgx/2;
lgx=y; y∈R
y²+y-6=0; D=1+24=25;
y₁₂=0,5(-1±5);
y₁=2; y₂=-3;
lgx=y₁;
lgx=2; x₁=10²=100;
lgx=-3;x₂=10⁻³=0,001
x₁=10²=100;
x₂=10⁻³=0,001;
x₁=100
x₂=0,001.
log_π_x+log_π_2+log_π_(8-x)>log_π_(x+27);
log_π_(x*2*(8-x)>log_π_(x+27);
log_π_(-2x²+16x)>log_π_(x+27);
log_π_(-2x²+16x)-log_π_(x+27)>0;
log_π_((-2x²+16x)/(x+27))>0;
π⁰>((-2x²+16x)/(x+27)); x≠-27
(-2x²+16x)/(x+27)<1;
(-2x²+16x)/(x+27)-1<0;
[-2x²+16x-x-27]/(x+27)<0;
[-3x²+15x-27]/(x+27)<0;
[3x²-15x+27]/(x+27)>0;
3x²-15x+27>0; D<0
x+27>0;x>-27
3x²-15x+27<0; D<0
x+27<0;x<-27
x∈]-∞;-27[∪]-27;+∞[
сил больше нет ((