1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма .
И правда. Пусть - сумма всех комбинаций по 1 ... по k элементов. Тогда
Т.к. числа отрицательны, то
Если хотя бы одно из , вся сумма равна -1.
В остальных случаях - всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что .
Y=(x+1)^2-2 Этот график получается из графика y1=x^2 с сдвига на вектор с координатами (-1;-2), т.е с сдвигом вдоль оси ох на 1 влево, и вдоль оси оу на 2 вниз. График является параболой, т.е нам достаточно пять точек. чтобы было проще мы возьмем координату вершины параболы, и точки пересечения с осями. Чтобы было легче раскроем скобки и приведем подобные: y=x^2+2x-1 Координаты вершины нахожим по формуле: X=-b/2a=-2/2=-1. Y=-2. Точки пересечения с осью ох, когда y=0; x^2+2x-1=0 D/4=5; т.к х-иррациональное число, то мы возьмем другие координаты. Точки пересечения с осью оу: х=0, у=-1. У нас есть две точки, нам нужно еще три. Выберем абсолютно любые х и найдем значение у. Я взяла х=-2; у=-1; Х=1, у=2; Х=-3, у=2. Теперь запишем это в таблицу значений. Х | -3 | -2 | -1 | 0 | 1
1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма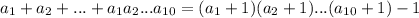
.
И правда. Пусть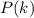
- сумма всех комбинаций по 1 ... по k элементов. Тогда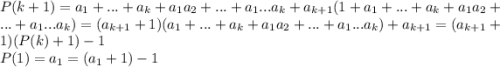 
Т.к. числа отрицательны, то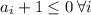
Если хотя бы одно из
, вся сумма равна -1.
В остальных случаях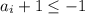
- всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что 
.
А тогда сумма могла равняться только -1