Заданный график функции y=x^2-2xy=x
2
−2x является параболой.
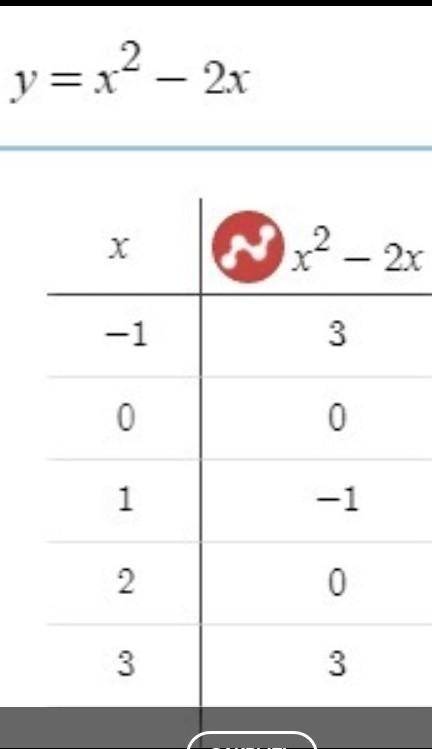
Для построения графика функции задаемся различными значениями Х и считаем значения Y
Например: пусть х = 0 , тогда y (0) = 0² - 2*0 = 0 и т.д.
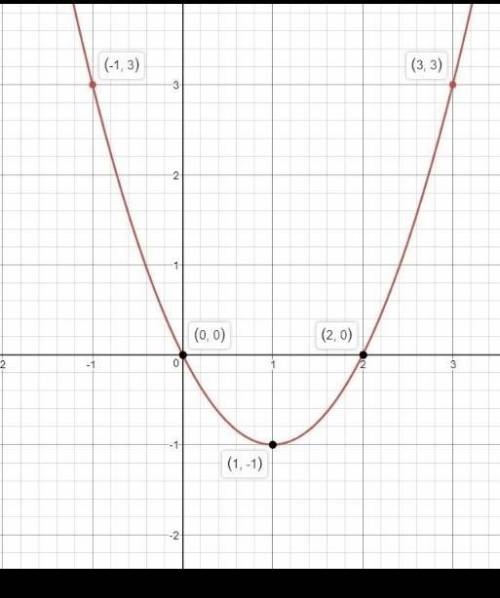
Другие точки для построения и сам график, представлены ниже
Б) Так как а=1 > 0 , то её ветви направлены вверх. Тогда слева, до вершины параболы - график убывает, а после вершины - возрастает.
Найдем вершину параболы
x_0 = - \frac{b}{2a} = - \frac{-2}{2*1} = 1x
0
=−
2a
b
=−
2∗1
−2
=1
Тогда можно окончательно записать:
на промежутке (- \infty ; \ 1](−∞; 1] - функция убывает
на промежутке [1 \ ; + \infty)[1 ;+∞) - функция возрастает.
А) наименьшее и наибольшее значения функции на отрезке [0; 3]
Учитывая, что вершина параболы x_0 =1x
0
=1 принадлежит данному отрезку, то в вершине будет наименьшее значение функции
y (1) = 1^2-2*1 = -1y(1)=1
2
−2∗1=−1
а в точке х=3 будет наибольшее значения функции
y (3) = 3^2-2*3 = 3y(3)=3
2
−2∗3=3
В) Hешите неравенства x^2-2x \leq 0x
2
−2x≤0
Если посмотреть на построенный график, то можно отметить, что парабола лежит ниже нуля на интервале от 0 до 2, тогда решение неравенства будет
0 \leq x \leq 20≤x≤2
ответ: сумма первых шести членом этой прогрессии равна 728
Объяснение:
Что бы найти сумму нужно воспользоваться формулой суммы первых n членов геометрической прогрессии Sn = b1*(1-q^n)/(1-q), где b1 - первый член геометрической прогрессии, q - знаменатель геометрической прогрессии.Чтобы найти сумму первых шести членов прогрессии нужно подставить в данную формулу первый член геометрической прогрессии b1 и знаменатель геометрической прогрессии q из условия задачи и подсчитать полученное выражение при n=6.
В условии задачи, b1 = 2, q = 3. В таком случае
S6 = b1*(1-q^6)/(1-q) = 2*(1-3^6)/(1-3) = 2*(1-3^6)/(1-3) = 2*(1-729)/(1-3) = 2*(-728)/(1-3)= 2*(-728)/(-2) = 728
7/6 4/5 6/10 1/2 7/15
Объяснение:
Приведем к общему знаменателю 30
35/30
24/30
18/30
14/30
15/30
и теперь сравним