
Объяснение:
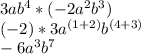
Пусть х часов-время за которое 1 бригада могла бы выполнить некоторую работу.
Тогда у часов-время за которое 2 бригада могла бы выполнить некоторую работу.
Известно,что Две бригады, работая вместе, могут выполнить некоторую работу за 12 часов.Отсюда следует,х+у=12.
Зная,что Первая бригада, работая одна, могла бы выполнить эту работу на 10 часов быстрее, чем вторая,отсюда следует,у-х=10.
Составим и решим систему уравнений:
х+у=12,
+
у-х=10;
2у=22,
у=10.
Значит,10 часов потребовалось бы первой бригаде для выполнения этой работы.
ответ:10 часов.
Пусть дано квадратное уравнение a•x²+b•x+c=0, a≠0. Теорема Виета доказывается для приведённых квадратных уравнений, то есть когда коэффициент a=1. А другие уравнения приводятся к такому виду.
Теорема Виета. Числа x₁ и x₂ являются корнями квадратного уравнения x²+p•x+q=0 тогда и только тогда, когда пара (x₁; x₂) является решением системы:
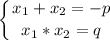
Теорема Виета утверждает, что квадратное уравнение и система одновременно разрешимы или неразрешимы. Ещё, теорема Виета даёт подбора корней:
Корни уравнения являются делителями свободного члена q!
Отсюда вывод: если корни уравнения целочисленные, то легко определить корни, если разложить свободный член q на множители.
Рассмотрим примеры.
Пример-1. Решить уравнение: x²–3•x+2=0.
Решение. По теореме Виета x₁ + x₂ = 3 и x₁ · x₂ = 2. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 2 = 1•2 = (–1)•(–2). Но из x₁ + x₂ = 3 видно, что корнями уравнения будут x₁=1 и x₂=2.
Пример-2. Решить уравнение: x²–6•x+8=0.
Решение. По теореме Виета x₁ + x₂ = 6 и x₁ · x₂ = 8. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 8 = 1•8 = 2•4 = (–1)•(–8) = (–2)•(–4). Но из x₁ + x₂ = 6 видно, что корнями уравнения будут x₁=2 и x₂=4.
Пример-3. Решить уравнение: x²+4•x+4=0.
Решение. По теореме Виета x₁ + x₂ = –4 и x₁ · x₂ = 4. Предполагая, что корни уравнения целочисленные рассмотрим разложение: 4 = 1•4 = 2•2 = (–1)•(–4) = (–2)•(–2). Но из x₁ + x₂ = –4 видно, что корнями уравнения будут x₁= –2 и x₂= –2.
Вот основная суть теоремы Виета.
3ab⁴ * (- 2a²b³) = 3 * (- 2) * a¹⁺² * b⁴⁺³ = - 6a³b⁷