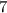(2+a)x^2+(1-a)x+a+5=0 Рассмотрим несколько ситуаций: 1)если старший коэффициент при x^2=0 ( при а=-2): 0*x^2+3x-2+5=0 3x+3=0 3x=-3 x=-1 Значит, a=-2 нам подходит 2) если средний коэффициент равен нулю ( при а=1): 3x^2+0*x+1+5=0 3x^2+6=0 3x^2=-6 - решений нет, значит а=1 нам не подходит. 3) если а не равно -2 и не равно 1, то перед нами квадратное уравнение, которое имеет хотя бы один корень тогда, когда дискриминант >=нуля: D= (1-a)^2-4(2+a)(a+5)>=0 1-2a+a^2-4(2a+10+a^2+5a)>=0 1-2a+a^2-4(a^2+7a+10)>=0 1-2a+a^2-4a^2-28a-40>=0 -3a^2-30a-39>=0 3a^2+30a+39<=0 | :3 a^2+10a+13<=0 a^2+10a+13=0 D=10^2-4*1*13=48 a1=(-10-4V3)/2=-5-2V3 a2=-5+2V3
20(x²-6x-9)²=x(x²-4x-9) (x²-6x-9)²-x(x²-4x-9)=0 (x²-6x)²-2(x²-6x)·9+9²-x³+4x²+9x=0 x⁴-12x³+36x²-18x²+108x+81-x³+4x²+9x=0 x⁴-13x³+22x²+117x+81=0 подставив вместо х=-1 убеждаемся, что 1+13+22-117+81=0 - верно Значит х=-1 - корень данного уравнения Делим x⁴-13x³+22x²+117x+81 на (х+1) получим х³-14х²+36х+81 Итак, x⁴-13x³+22x²+117x+81=(х+1)·(х³-14х²+36х+81) корни многочлена х³-14х²+36х+81 следует искать среди делителей свободного коэффициента 81
Это числа ±1;±3;±9 Подставим х=9 и убеждаемся, что 9³-14·9²+36·9+81=81(9-14+4+1)=81·0=0 х=9 - корень данного уравнения х³-14х²+36х+81 делим на (х-9) получим х²-5х-9 Осталось разложить на множители последнее выражение х²-5х-9=0 D=25+36=61 x=(5-√61)/2 или х=(5+√61)/2
Окончательно x⁴-13x³+22x²+117x+81=0 ⇒(х+1)·(х³-14х²+36х+81)=0⇒(х+1)(х-9)(х²-5х-9)=0⇒ х₁=-1 или х₂=9 или x₃=(5-√61)/2 или х₄=(5+√61)/2
ответ: