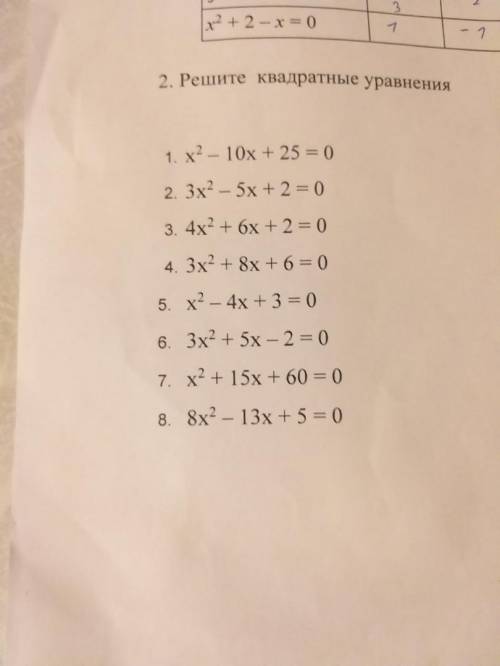
Объяснение:
а) 4x^4-8x^2+4-4x^6-4x^5+4x^4+8x^3+4x^6+4x^5-8x^3-2=8x^4-8x^2+2
четвертая степень
б) Запишем 8x^4-8x^2+2 как 8x^2(x^2-1)+2
Для случая |х| ∈ [0,1] произведение обращается в 0, а выражение равно 2. Двойка делится на 2, что и требовалось доказать.
Для случая |x| ≥ 2, x² может быть четным или нечетным. Если x² - четное, то (x² - 1) - нечетное. Произведение x² (x² -1) - всегда четное, умножение на 8 эту четность сохраняет, как и суммирование с числом 2. Таким образом выражение всегда четное, то есть делится на 2, ч.т.д.
в) Поскольку х возводится в четные степени (четвертую и вторую), то 8 x^4 - всегда положительное число. А поскольку речь о целых числах, то для любых |x|≥2 8x^4 будет больше, чем 8x², то есть их разница будет положительной.
В случаях, |x| ∈ [-1,1], при х = 0 оба первых слагаемых обращаются в нуль и остается только 2, положительное число, а при х = -1 или х = 1, сумма первых слагаемых обращается в 0, тогда значение выражения также становится равно 2, положительному числу.
Так мы доказали, что для любых целых х наше выражение всегда положительно.
1) 
, 
, 
.
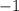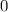2) , 
.
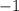Объяснение:
1) По утверждению, обратному лемме Ферма, в точке экстремума функции значение её производной равно нулю. Отсюда следует, что для нахождения точки экстремума функции следует сначала найти производную функции, а затем найти точки, в которых она равна нулю. Они и будут являться точками экстремума исходной функции.
Для данной функции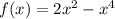 
найдём производную:
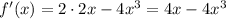. (применены правила: 
, 
)
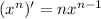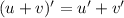Решим теперь уравнение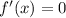 
:
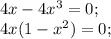
Отсюда следует, что или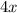 
равно нулю, или 
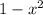равно нулю.
Первое:
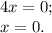
Второе:
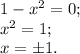
Получается, что точками экстремума функции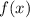 
являются 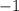, 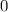и .
2) Аналогично первому заданию, для данной функции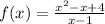 
найдём производную:
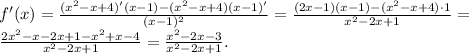(применены правила: , 
, 
, , 
)
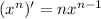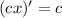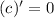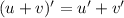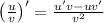Решим теперь уравнение :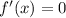
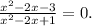
Из него следует, что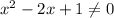 
, а также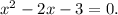 
Для первого:
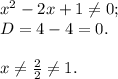
Для второго:
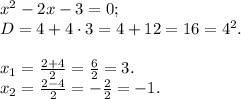
Все 
удовлетворяют условию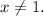 
Получается, что точками экстремума функции 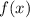являются 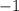и .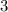
(x-5)²=0
x-5=0
x=5
Объяснение:
все есть в пхотомеч