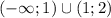
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
![7^{ax^2-2x}-7^{x^2-1}=\sqrt[7]{2x-ax^2}-\sqrt[7]{1-x^2} \\7^{ax^2-2x}-\sqrt[7]{2x-ax^2}=7^{x^2-1}-\sqrt[7]{1-x^2}\\7^{ax^2-2x}+\sqrt[7]{ax^2-2x} =7^{x^2-1}+\sqrt[7]{x^2-1}](/tpl/images/4771/4253/b4ecf.png)
Рассмотрим функцию ![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png)
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
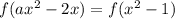
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
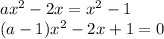
Если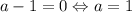 
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если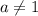 
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
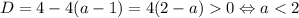
Учитывая, что 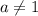, получаем ответ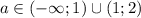 
где х, y - некоторые натуральные числа
Предположим что
тогда из второго соотношения (2) следует что
где k - некоторое натуральное число
откуда
а значит число |16a-9b| сложное если
и
Рассмотрим варианты
1)
что невозможно - два последовательных натуральных числа не могут быть квадратами натуральных чисел
(доказательство єтого факта
=>x=1; y=0
)
2)
=> k - ненатуральное -- невозможно
3)
=> k - ненатуральное - невозможно
тем самым окончательно доказали,что исходное утверждение верно.
Случай когда
Учитывая симметричность выражений a+b=b+a, ab=ba
доказывается аналогично.
Доказано