В 512 раз
Объем правильного тетраэдра вычисляется по формуле:
где a - величина ребра в принятых единицах измерения
В увеличенном тетраэдре ребро (назовем его b) составляет 8a
подставляя, заменяя и деля увеличенный объем на сравниваемый (с ребром b выраженным через значение a, то есть b = 8a) получаем, что увеличение объема в данном случае будет составлять 8³ = 512 (ед.)
То есть в общем случае:
увеличение/уменьшение объема правильного тетраэдра пропорционально кубу единицы увеличения/уменьшения его ребра
ctgx(ctgx+1)=0
ctgx=0 или ctgx+1=0
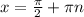ctgx=-1
n=-1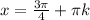 
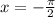k=-1
n=0 
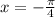
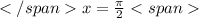k=0
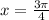
т.е. на данном промежутке находятся 4 корня
x1 * x2 = 63
=> x1=7 и x2=9