Задание удобно решать графически.Надо начертить график ф-ции у=|x-1|+|x+1| и у=а.
Знаки |x-1| - - - (-1) - - - (1) + + +
Знаки |x+1| - - - (-1) + + + (1) + + +
Рассматриваем три интервала.
-∞<х≤ -1 ⇒ у=-х+1-х-1=-2х Строим эту прямую y=-2x при х∈(-∞,-1].
-1<x≤1 ⇒ y=-x+1+x+1=2 ⇒Прямую у=2 строим при х∈(-1,1]
1<х<∞ ⇒у=х-1+х+1=2х . Строим прямую у=2х при х∈(1,∞)
Прямые строят только в тех пределах изменения переменной х, в которой это указано.Остальные части прямых стирают.
По графику будет видно, что прямая у= а,которая параллельна оси ОХ не будет перес екать график ф-ции у=|x-1|+|x+1| при а<2.А значит, при а<2 уравнение не имеет корней
ТЕОРИЯ (это важно):
Сначала нужно найти начало координат, то есть вершину параболы с учётом её сдвига. Для этого находим координаты x₀, y₀ вершины O параболы (по осям OX и OY соответственно), вычисляем их по специальным формулам:
. O(x₀;y₀), где x₀ — координата по оси OX, y₀ — координата по оси OY, O — начало координат.Потом, когда найдена вершина, строим график той функции, из которой получена данная нам в условии функция, начиная от вершины. Важно понимать: если нам дана функция, например, y=4x²+2x+1, то после нахождения вершины параболы для данной функции строим, начиная от вершины, график функции y=4x² — смотрим на коэффициент (число) перед x². Так, функция y=2x²-1x+2 получена из функции y=2x², а y=x²+4x+1 получена из функции y=x². Задача коэффициентов b и c — «сдвинуть» вершину параболы на определённую координату. Таким образом, функция y=ax²+bx+c называется квадратичной, график — парабола, получена из функции y=ax² (где a — коэффициент перед x²) сдвигом вдоль осей координат на m по оси OY и на L по оси OX. Если a>0, ветви параболы направлены вверх; если a<0, ветви параболы направлены вниз.Квадратичная функция y=x²+4x+1. График — парабола, ветви направлены вверх (a>0), получена из функции y=x² сдвигом вдоль осей координат на 3 единичных отрезка вниз и на 2 единичных отрезка влево. 1. Найдём координаты начала координат: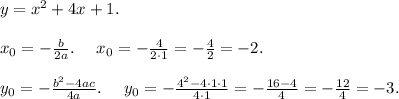 
Значит, O(-2;-3).
2. Построим график функции y=x². Строим таблицу значений:x=1 x=2 x=3
y=1 y=4 y=9
График на картинке
АЛГОРИТМ ПОСТРОЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ y=ax²+bx+c:
Найти координаты начала координат (вершины параболы).Определить, из какой функции получена данная в условии функция.Строим таблицу значений для той функции, из которой получена данная нам в условии функция.Отмечаем на чертеже точку вершины параболы, построить оси.Построить и подписать параболу.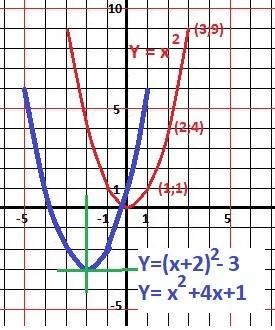
РешениеSin²x + 5sinxcosx + 2cos²x = - 1 Sin²x + 5sinxcosx + 2cos²x = - sin²x - cos²x
2sin²x + 5sinxcosx + 3cos²x = 0 делим на cos²x ≠ 02tg²x + 5tgx + 3 = 0
tgx = t
2t² + 5t + 3 = 0
D = 25 - 4*2*3 = 1
t₁ = (- 5 - 1)/4 = - 6/4 = - 3/2 = - 1,5
t₂ = (- 5 + 1)/4 = - 1
1) tgx = - 3/2
x₁ = - arctg(1,5) + πk, k ∈ Z
2) tgx = - 1
x₂ = - π/4 + πn, n ∈ Z
Если память не изменяет, то как-то так
Объяснение: