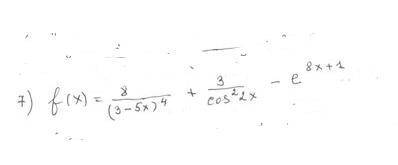
Объяснение:
х км/ч — скорость течения реки,
(х + 20) км/ч — собственная скорость теплохода ( скорость в стоячей воде)
Скорость движения теплохода по течению реки будет:
х+(х+20)=2х+20 км/час
Скорость движения теплохода против течения реки будет :
(х+20)-х=20 км/час
Значит можем найти время движения по течению и против течения:
время движения по течению
60 / (2х + 20) час.
против течения
60 / 20 = 3 час.
Если всего за 5,5 часа , то
5,5 - 3 = 2,5 час. - движение по течению
Отсюда :
60 / (2х + 20) = 2,5.
2,5 * (2х + 20)=60
5х + 50=60
5х=10
х = 2 км/час скорость течения реки
2 + 20 = 22 км/ч. собственная скорость теплохода ( скорость в стоячей воде)
Объяснение:
х км/ч — скорость течения реки,
(х + 20) км/ч — собственная скорость теплохода ( скорость в стоячей воде)
Скорость движения теплохода по течению реки будет:
х+(х+20)=2х+20 км/час
Скорость движения теплохода против течения реки будет :
(х+20)-х=20 км/час
Значит можем найти время движения по течению и против течения:
время движения по течению
60 / (2х + 20) час.
против течения
60 / 20 = 3 час.
Если всего за 5,5 часа , то
5,5 - 3 = 2,5 час. - движение по течению
Отсюда :
60 / (2х + 20) = 2,5.
2,5 * (2х + 20)=60
5х + 50=60
5х=10
х = 2 км/час скорость течения реки
2 + 20 = 22 км/ч. собственная скорость теплохода ( скорость в стоячей воде)
Совокупность всех первообразных функции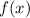 называют неопределенным интегралом:
называют неопределенным интегралом:
где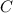 — произвольная постоянная.
— произвольная постоянная.
Тогда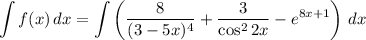
Теорема: если функции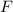 и
и 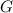 являются соответственно первообразными функций
являются соответственно первообразными функций 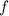 и
и 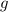 на промежутке
на промежутке 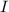 , то на этом промежутке функция
, то на этом промежутке функция 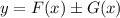 является первообразной функции
является первообразной функции 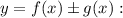
где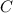 — произвольная постоянная.
— произвольная постоянная.
Тогда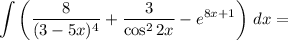
Теорема: если функция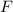 является первообразной для функции
является первообразной для функции 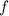 на промежутке
на промежутке 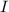 , а
, а 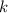 — некоторое число, то на этом промежутке функция
— некоторое число, то на этом промежутке функция 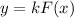 является первообразной функции
является первообразной функции 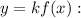
Тогда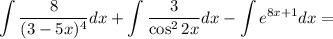
Теорема: если функция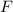 является первообразной для функции
является первообразной для функции 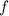 на промежутке
на промежутке 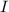 , а
, а 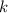 — некоторое число, отличное от нуля, то на соответствующем промежутке функция
— некоторое число, отличное от нуля, то на соответствующем промежутке функция 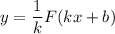 является первообразной функции
является первообразной функции 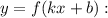
где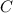 — произвольная постоянная.
— произвольная постоянная.
Найдем каждый интеграл по отдельности:
Получаем: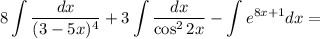
Таким образом, общий вид первообразных для функции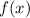 имеет вид:
имеет вид:
ответ: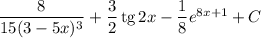
Использованные формулы интегрирования: