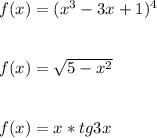 Очень нужно свериться.Решение с онлайн калькуляторов не предлагайте.
Очень нужно свериться.Решение с онлайн калькуляторов не предлагайте.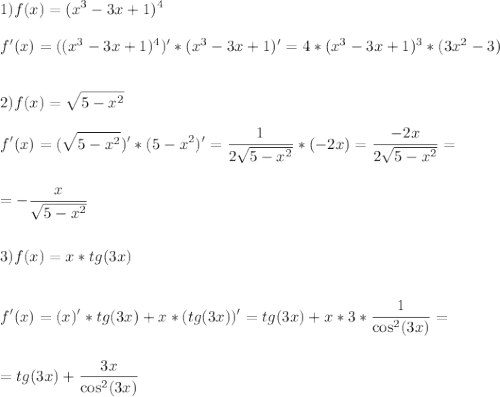
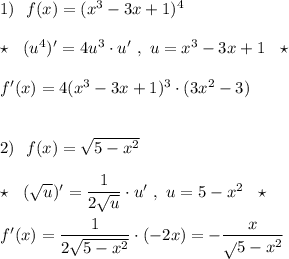
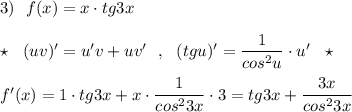
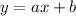 - a угловой коэффициент,b точка пересечения прямой с осью у.
- a угловой коэффициент,b точка пересечения прямой с осью у. , следовательно, данные прямые пересекают ось у в начале координат.
, следовательно, данные прямые пересекают ось у в начале координат.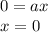
 - область определения.
- область определения.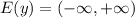 - область значений.
- область значений.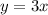
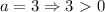 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.

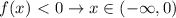

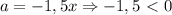 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

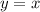
 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


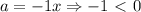 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

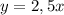
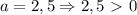 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)




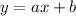 - a угловой коэффициент,b точка пересечения прямой с осью у.
- a угловой коэффициент,b точка пересечения прямой с осью у. , следовательно, данные прямые пересекают ось у в начале координат.
, следовательно, данные прямые пересекают ось у в начале координат.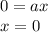
 - область определения.
- область определения.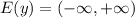 - область значений.
- область значений.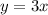
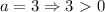 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.

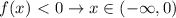

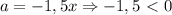 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

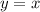
 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


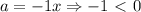 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

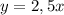
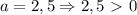 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)



