Объяснение:
№8
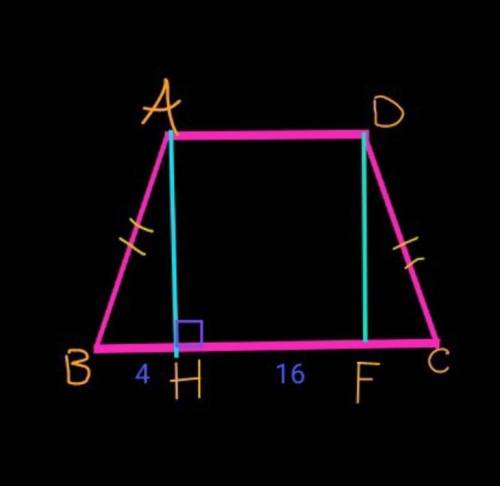
Дано:
АН – высота;
ВН=4 дм;
НС=16 дм;
АВ=DC.
Проведём высоту DF к стороне ВС.
Рассмотрим прямоугольные треугольники АНВ и DFC.
АВ=DC по условию;
Так как основания трапеции паралельны, а АН и DF высоты, проведенные к основанию ВС, то АDFH прямоугольник. Следовательно АН и DF равны.
Тогда прямоугольные треугольники АНВ и DFC равны по гипотенузе и катету. Следовательно FC=BH=4;
HF=HC–FC=16–4=12 (дм).
Так как АDFH – прямоугольник (доказано ранее), то AD=HF=12 (дм)
ответ: Б) 12 дм.
№9
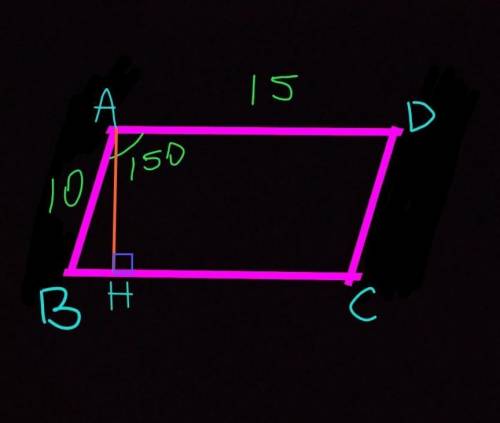
Рассмотрим треугольник АВН.
Так как АН – высота (по условию), то угол АНВ=90, тогда треугольник АВН прямоугольный.
Сумма углов при одной его стороне равна 180°, тогда:
угол ABH= 180°– угол BAD=180°–150°=30°
В прямоугольном треугольнике напротив угла в 30° лежит катет вдвое меньший гипотенузы, тоесть:
АН=АВ÷2=10÷2=5 см.
S=ah, где S–площадь паралелограмма, а– сторона паралелограмма, h– высота паралелограмма.
Подставим значения:
S=15*5=75 см²
ответ: В) 75 см²
А получит 100 рупий (А+100) ---а В их отдал (В-100)
А+100 = 2*(В-100) ---А вдвое богаче (у В денег меньше)
А отдаст 10 рупий (А-10) ---а В их получит (В+10)
6*(А-10) = В+10 ---В вшестеро богаче (у А меньше денег)
получили систему из двух уравнений
из первого выразим А = 2В - 200 - 100 = 2В - 300
подставим во второе 6*(2В-300 - 10) = В + 10
12В - 1860 = В + 10
11В = 1870
В = 1870/11 = 170
А = 2В - 300 = 2*170 - 300 = 340 - 300 = 40
ответ: у А 40 рупий, у В 170 рупий
ПРОВЕРКА: 40+100 = 140 170-100 = 70 140 = 70*2
40-10 = 30 170+10 = 180 30*6 = 180