Question

Докажите классическое неравенство: $\frac{2}{\frac{1}{a} +\frac{1}{b} } \leq \sqrt{ab}$

Answer 1

Объяснение:

Для отрицательных a и b неравенство очевидно. Докажем для случая a,b>0:

$\frac{2}{\frac{1}{a}+\frac{1}{b}} \leq \sqrt{ab};$

$\frac{2ab}{a+b} \leq \sqrt{ab};$

$\frac{a+b}{2ab}\geq \frac{1}{\sqrt{ab}};$

$a+b \geq 2\sqrt{ab};$

$a-2\sqrt{ab}+b\geq 0;$

$(\sqrt{a}-\sqrt{b})^2\geq0.$

Последнее неравенство выполняется для любых неотрицательных a и b, что с учетом ОДЗ исходного неравенства говорит о том, что оно справедливо для любых положительных a и b, причем равенство достигается при a=b>0

Answer 2

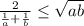
(см. объяснение)

Объяснение:

$\frac{2}{ \frac{1}{a} + \frac{1}{b} } \leqslant \sqrt{ab} \\ 2 \leqslant \frac{ \sqrt{ab} }{a} + \frac{ \sqrt{ab} }{b} \\ 2 \leqslant \sqrt{ \frac{b}{a} } + \sqrt{ \frac{a}{b} } \\ \sqrt{ \frac{b}{a} } - 2+ \sqrt{ \frac{a}{b} } \geqslant 0$

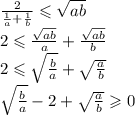
Рассмотрим внимательно получившееся выражение: это формула сокращённого умножения: разность квадратов. Учитывая это, перепишем выражение:

$( \sqrt[4]{ \frac{b}{a} } - \sqrt[4]{ \frac{a}{b} } ) {}^{2} \geqslant 0$

Выражение в квадрате всегда не отрицательно, поэтому равенство выше всегда верно.

Доказано.