1) Любое чётное число можно записать в виде 2n, n- натуральное число при n=1 получим первое четное число, равное 2 при n=2 - второе число, равное 4
при n=10 - десятое число, равное 20 при n=99 - девяносто девятое число, равно 198 2) Любое нечётное число можно записать в виде 2k-1, k - натуральное число при k=1 получим первое нечетное число, равное 2·1-1=1 при k=2 - второе число, равное 2·2-1= 3
при k=12 - двенадцатое число, равное 2·12-1=23
при k=77 - семьдесят седьмое число, равное 2·77-1=153.
Пусть т первый корень уравнения, тогда 2т второй корень уравнения. Подставив значения корней в уравнение ( т и 2т ) получаем систему 2х уравнений с неизвестными т и к. Решив ее, найдем значения первого корня и кожффициента к.
2т^2-кт+4=0 8т^2-2кт+4=0
-4т^2+2кт-8=0 8т^2-2кт+4=0
4т^2-4=0 2т^2-кт+4=0
т=1 или т= -1
Если т=1 то к=6, если т= -1 то к= -6.
Таким образом получили 2 случая:
1) при к=6 корни уравнения ( т и 2т ) равны 1 и 2
2) при к= -6 корни уравнения ( т и 2т ) равны -1 и -2
![Решите систему неравенств : x²+3x+4>0 [x²-2x-1]<0](/tpl/images/1353/3416/ce484.jpg)
(см. объяснение)
Объяснение:
Рассмотрим 1-ую строку системы:
Т.к. коэффициент при x² - положительное число, то x любое число.
Рассмотрим 2-ую строку системы:
Поскольку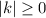
, то у неравенства нет решений.
Значит у системы нет решений.