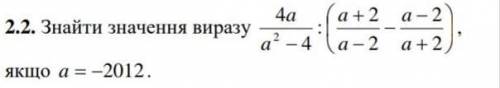
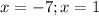
Объяснение:
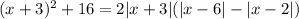
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение 
и перенесем слагаемое 
в левую часть:
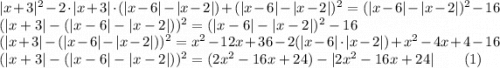
1) 
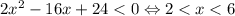
Тогда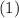 
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2) 
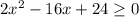
Возможны 2 случая:
2.1)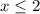 
Тогда 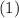примет вид
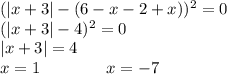
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2) 
Тогда 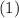примет вид
То есть корень не принадлежит рассматриваемому интервалу.
тогда второе число, пропорциональное числу 2 равно 2х.
Т.к. сумма трёх чисел равна 18,то третье число равно 18-х-2х=18-3х
По условию, произведение этих трёх чисел должно принимать наибольшее значение. Применим производную для решения задачи:
f(x)=x*2x*(18-3x)=2x²(18-3x)=36x²-6x³
f `(x)=(36x²-6x³)`=36*2x-6*3x²=72x-18x²=18x(4-x)
f `(x)=0 при 18x(4-x)=0
- + -
04
min max
↓ ↑ ↓
x=4
2x=2*4=8
18-4-8=6
ответ: 4; 8; 6 - искомые числа