1) D(y) = [0; + ∞) \ {1; 2/3}
2) D(y) = [–3; 3] \ {–2}.
Объяснение:
Области определения тут могут быть ограничены следующим: определением корня чётной степени, а также тем, что знаменатель в дроби не равен нулю.
1) Присутствует
![\sqrt[4]{x}](/tpl/images/1100/2819/19eed.png)
Значит х≥0.
Далее знаменатель ≠ 0. Кстати, это ещё и корень с чётной степенью (2), т.е. есть ещё и ограничение, что
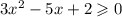
А когда корень из числа равен нулю? Тогда и только тогда, когда само подкоренное выражение равно нулю. И да, всё решение рассматриваем на множестве действительных (они же вещественные) чисел.
Значит нужно решить квадратное уравнение, тогда его корни и будут недопустимыми значениями.
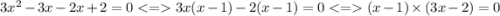
Т. о. получается совокупность – либо х = 1, либо 3х = 2. Значит либо х = 1, либо х = 2/3. Так как оба корня является решением квадратного уравнения, при них выражение не будет определено (деление на ноль) т.е. в область определения следует записать: х ≠ 1, х≠2/3.
Т.о. следующие ограничения: х≥0, х ≠ 2/3, х≠1. Все они должны выполняться одновременно, значит D(y) = [0; + ∞) \ {1; 2/3}. Если что, D – обозначение области определения функции, \ – операция "вычитания" из множества.
2) Тут знаменатель тоже не должен быть равен нулю т.е. х + 2 ≠ 0 <=> х ≠ –2.
И также в числителе корень с чётной степенью, значит подкоренное выражение
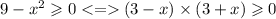
Предлагаю решить методом интервалов, так как здесь сравнение с нулём.
Необходимо начертить координатную ось с соответствующей подписью (в данном случае х), далее отметить значения, при которых один из множителей обращается в ноль – здесь это х = 3 и х = – 3. Так получились три области, в которых значение произведения/выражения данного одного знака (больше или меньше нуля) Далее подставляем в х огроооомное число, явно превышающее 3 (обозначенное число-граница) т.к. так удобнее и узнаём, больше или меньше 0 это произведение – оно меньше, значит ставим минус в той области. Далее можно не подставлять, а понять, что так как нет других множителей и множителя в чётной степени, знак выражения в областях будет чередоваться. Числа-границы нужно учитывать в ответ (закрашивая), если выражение может быть равно нулю (т.е. ≥0) Таким образом решением является следующее множество: [–3; 3]
Все условия/ограничения должны выполняться, т.е. получается система из х≠–2 и 3 ≥ х ≥–3. Значит область определения D(y) = [–3; 3] \ {–2}.


1) D(y) = [0; + ∞) \ {1; 2/3}
2) D(y) = [–3; 3] \ {–2}.
Объяснение:
Области определения тут могут быть ограничены следующим: определением корня чётной степени, а также тем, что знаменатель в дроби не равен нулю.
1) Присутствует
![\sqrt[4]{x}](/tpl/images/1100/2819/19eed.png)
Значит х≥0.
Далее знаменатель ≠ 0. Кстати, это ещё и корень с чётной степенью (2), т.е. есть ещё и ограничение, что
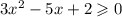
А когда корень из числа равен нулю? Тогда и только тогда, когда само подкоренное выражение равно нулю. И да, всё решение рассматриваем на множестве действительных (они же вещественные) чисел.
Значит нужно решить квадратное уравнение, тогда его корни и будут недопустимыми значениями.
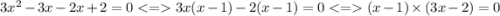
Т. о. получается совокупность – либо х = 1, либо 3х = 2. Значит либо х = 1, либо х = 2/3. Так как оба корня является решением квадратного уравнения, при них выражение не будет определено (деление на ноль) т.е. в область определения следует записать: х ≠ 1, х≠2/3.
Т.о. следующие ограничения: х≥0, х ≠ 2/3, х≠1. Все они должны выполняться одновременно, значит D(y) = [0; + ∞) \ {1; 2/3}. Если что, D – обозначение области определения функции, \ – операция "вычитания" из множества.
2) Тут знаменатель тоже не должен быть равен нулю т.е. х + 2 ≠ 0 <=> х ≠ –2.
И также в числителе корень с чётной степенью, значит подкоренное выражение
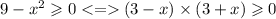
Предлагаю решить методом интервалов, так как здесь сравнение с нулём.
Необходимо начертить координатную ось с соответствующей подписью (в данном случае х), далее отметить значения, при которых один из множителей обращается в ноль – здесь это х = 3 и х = – 3. Так получились три области, в которых значение произведения/выражения данного одного знака (больше или меньше нуля) Далее подставляем в х огроооомное число, явно превышающее 3 (обозначенное число-граница) т.к. так удобнее и узнаём, больше или меньше 0 это произведение – оно меньше, значит ставим минус в той области. Далее можно не подставлять, а понять, что так как нет других множителей и множителя в чётной степени, знак выражения в областях будет чередоваться. Числа-границы нужно учитывать в ответ (закрашивая), если выражение может быть равно нулю (т.е. ≥0) Таким образом решением является следующее множество: [–3; 3]
Все условия/ограничения должны выполняться, т.е. получается система из х≠–2 и 3 ≥ х ≥–3. Значит область определения D(y) = [–3; 3] \ {–2}.


Необходимо было решить 2 первые задачи из документа, но я решил ещё и параметр, который мне понравился.
12. Необходимо решить уравнение
Формула двойного угла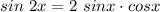
А также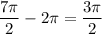 , как известно, добавление или вычитание целого периода из аргумента тригонометрической функции ничего не меняет.
, как известно, добавление или вычитание целого периода из аргумента тригонометрической функции ничего не меняет.
Так как в выражении в скобках присутствует половинный аргумент при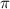 , то косинус поменяется на синус, знак будет отрицательным, потому что если считать, что
, то косинус поменяется на синус, знак будет отрицательным, потому что если считать, что  находится в первой координатной четверти, то при вычислении выражения в скобках значение будет в третьей четверти, где обе функции отрицательны.
находится в первой координатной четверти, то при вычислении выражения в скобках значение будет в третьей четверти, где обе функции отрицательны.
Получаем уравнение , которое поделим на
, которое поделим на 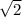
Первая часть готова, осталось проанализировать каждую серию решений на принадлежность промежутку![\displaystyle \bigg[-\pi; \frac{3\pi}{2}\bigg]](/tpl/images/1354/0763/31165.png)
Здесь подойдут
Анализируем 2 оставшиеся серии:
Здесь уже необходимо рассматривать отдельно.
Первое с "+" возьмем: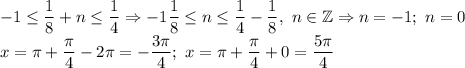
В последней серии решений та же логика, просто исходно дробь будет со знаком "-", значит, в обе части двойного неравенства пойдет с "+"
Теперь можно записывать ответ:
Переходим к 13. Это неравенство.
Сразу видно, что можно заменить на переменную, и тогда неравенство станет куда проще.
можно заменить на переменную, и тогда неравенство станет куда проще.
Если знаменатель больше нуля, то и неравенство будет больше 0. Особый случай - когда числитель равен 1, но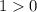 , поэтому решением этого неравенство является
, поэтому решением этого неравенство является 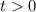
Возвращаемся к замене и решаем относительно :
:
Тогда получается, что и для любого неравенство выполняется.
неравенство выполняется.
ответ: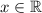
Решение задачи с параметром прикрепляю отдельным документом, так как мне не хватило ограничения на 5000 символов, к сожалению (