Question

Якою цифрою закінчується число 99^99^9

Answer 1

$99^{99^9}$

Начнем возводить число, оканчивающееся на 9, в натуральные степени:

$(...9)^2=(...9)\cdot(...9)=...1$

$(...9)^3=(...9)^2\cdot(...9)=(...1)\cdot(...9)=...9$

$(...9)^4=(...9)^3\cdot(...9)=(...9)\cdot(...9)=...1$

Получаем повторение в цикле: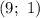 $(9;\ 1)$.

Заметим, что при возведении такого числа в нечетную степень мы получаем число, оканчивающееся на 9, а при возведении в четную степень - число, оканчивающееся на 1.

Таким образом, число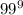 $99^9$ оканчивается на 9, а следовательно, является нечетным. Значит, при возведении числа 99 в степень 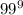$99^9$также получится число, оканчивающееся на 9.

$99^{99^9}=99^{...9}=...9$

ответ: 9