Все четырёхзначные числа из цифр  , без повторения цифр:
, без повторения цифр:
1023
1032
1203
1230
1320
1302
2013
2031
2103
2130
2301
2310
3012
3021
3102
3120
3201
3210
Всего: 18 чисел
✓РЕШЕНО МУДROST✓Рассмотрим прямоугольник mknz.
mo = on, ko = oz т.к. диагонали прямоугольника в точке пересечения делятся пополам
ma = ao, oc = cn по условию.
ao = mo : 2, oc = on : 2 по условию.
mo = on из этого следует, что ao = oc
kb = bo, od = dz по условию.
bo = ko : 2, oc = oz : 2 по условию.
ko = oz из этого следует, что bo = od
рассмотрим четырёхугольник abcd
диагональ bd в точке о делит диагональ ac на 2 равных отрезка
диагональ ac в точке о делит диагональ bd на 2 равных отрезка
ответ: четырёхугольник abcd является прямоугольником т.к. его диагонали делятся пополам в очке пересечения.
Объяснение:
1) Дано: F(x)=x²+4 - функция, Хо = 1.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 2*x
Вычисляем в точке Хо = 1.
F'(1) = 2 - производная и F(1) = 5 - функция.
Записываем уравнения прямой.
Y = 2*(x - 1) + (5) = 2*x + 3 - касательная - ОТВЕТ
Рисунок к задаче в приложении.
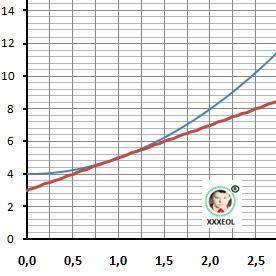
2) Дано: F(x)=2*x²+ x - функция, Хо = 2.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 4*x + 1.
Вычисляем в точке Хо = 2.
F'(2) = 9 - производная и F(2) = 10 - функция.
Записываем уравнения прямой.
Y = 9*(x - 2) + (10) = 9*x -8 - касательная - ОТВЕТ
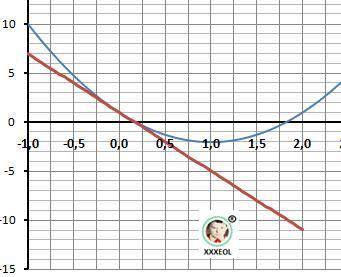
3) Дано: F(x)=3*x² -6*x +1 - функция, Хо = 0.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 6*x -6.
Вычисляем в точке Хо = 0.
F'(0) = -6 - производная и F(0) = 1 - функция.
Записываем уравнения прямой.
Y = -6*(x - 0) + (1) = -6*x + 1 - касательная - ОТВЕТ
Рисунок к задаче в приложении.
18
Объяснение:
Первой цифрой может быть 1, 2 и 3( 0 первой быть не может) то есть 3 варианта.
Второй цифрой может быть 0 и ещё две цифри, кроме той которую мы поставили на первое место. Опять 3 варианта
Третья - 2 варианта, а четвертая 1 вариант.
Итого 3*3*2*1 = 18